darkpanda
Dark Prince
- Joined
- Oct 28, 2007
- Messages
- 844
I was in a bit of a rush when I posted a simple patch to make all/none map squares special. At that time, I was looking at the "Check Special Resource" for completely different reasons (reviewing the map drawing code).
But right after posting it, I started to wonder: in what more sophisticated/interesting ways could this routine be altered?
To investigate possibilities, I started to explore 3 different approaches:
Hereunder, I provide more details about each approach (only 1. completed thus far).
The 2 formulae to determine whether or not a map square contains a special resource or a hut are re-stated hereunder:
The first few elements of those boolean formulae are simply checking for other external conditions (square not in poles, hut not already visited, etc).
The last operand of both formulae are the ones that control those very peculiar patterns that CIV players quickly get familiar with:

Special resource pattern

Huts pattern

1.1. In-depth pattern analysis
Before altering those formulae, let's try to make some sense out of them (if you're not interested, you can skip this part and go to 1.2. directly).
First, let's look at the left operand, which is identical for both formulae:
X and Y are the coordinates of the map square. If we exclude the poles, they range, respectively, from 0 to 79 (included) and from 2 to 47 (included). The square with coordinates (0,0) is the top-left corner of the map, and from this square, the X and Y coordinates increase 1 by 1 horizontally towards the right (X) and vertically towards the bottom (Y). It can be represented as follows:

The meaning of N MOD 4 is the value of integer N modulo 4, or in other words, the remainder of the integer division of N by 4. One of the properties of the modulo operation is that it produces cyclical values when given a linear input range of integers.
Typically:
With this property in mind, we can get the intuition that if X MOD 4 and Y MOD 4 are both cyclical, then (X MOD 4)*4 + (Y MOD 4) is also going to be cyclical, all the more that (X MOD 4) is multiplied by 4, which happens to be modulo divisor.
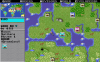
When computing (X MOD 4)*4 + (Y MOD 4) for all map squares (X,Y), we immediately see a cyclical pattern appear, as highlighted in blue in the grid below:

The cyclic pattern is a 4x4 area that contains values from 0 to 15, ordered from top to bottom and left to right.
In other words, the left operand divides the map in a set of identical 4x4-square areas, each area containing all values from 0 to 15.
Now, let's look at the right operands:
Here again, there is a strong similarity between both formulae, the only differences being the final MOD divisor (16 vs 32) and the addition of 8 for the Hut formula.
Let's look at the identical part first: (X/4)*13 + (Y/4)*11 + TMW
Here, N/4 yields the quotient of the integer division of N by 4. When applied to a continuous range of values like 0, 1, 2, 3, 4, 5, 6, ..., this operation is guaranteed to return the same result for 4 consecutive values:
Again, when applied to both X and Y, we can foresee that this formula will work at a the level of 4x4-square areas:

We also see in the picture above that X/4 and Y/4 are symmetrical, and this is always an issue when trying to design a random pattern.
This is why CIV developers multiply X/4 by 13 and Y/4 by 11. The reason for choosing 11 and 13 as multipliers is that they are both prime numbers whose smallest common mulitplicant is, thus, their own product 11 x 13. Another reason is that they result in a rather nice and even pattern...
This beats symmetry because the smallest X and Y necessary for X/4*13 being equal to, and thus symmetrically exchangeable with Y/4*11, are X = 11*4 = 44 and Y = 13*4 = 52, which never happens since Y is always smaller than 52.
So this guarantees that X/4*13 + Y/4*11 always yields different results for all values of X and Y within the map.
In this part of the formula, the addition of the Terrain Master Word (TMW) brings variation in the pattern from game to game.
Looking only at the special resource formula, the final step is the MOD 16 operation, which effectively gets the value of X/4*13 + Y/4*11 + TMW within the range [0..15]:

Since we are only dealing with values between 0 and 15 though, we cannot avoid having a pattern repetition in those right operand values, as highlighted below, where all colored areas are identical:

Now, since the resulting value of both operands are within the range [0..15], there is a guaranteed single match between both operands for every 4x4 area. In other words, there is 1 and only 1 square for each 4x4-square area on the map that will make the special resource formula true:

Matching with the first operand, we can see how the right operand pattern repetition results in the repetition of the special resource pattern as well:

Now let's look a the right operand of the hut pattern formula: ((X/4)*13 + (Y/4)*11 + TMW + 8) MOD 32
Compared to the special resource formula, the addition of 8 plays only a little role, which is to shift the pattern compared to the special resrouce pattern, otherwise, without this "+8", every hut square would also be a special resource square.
The real difference lies in the 32 MOD divisor (0x1F) instead of 16 (0xF) for special resource: the MOD 32 operation will cast the right operand values for the 4x4 areas ( (X/4)*13 + (Y/4)*11 + TMW + 8 ) into the [0..31] range, instead of [0..15] for the special resource pattern.
Since the left operand values' range is only [0..15], this means that 4x4 areas for which the right operand value ranges from 16 to 31 will not contain any square for which the hut formula is true, i.e. those 4x4 areas will not contain any hut square. Those areas have a gray background in the picture below:

On average, this cuts by half the potential number of huts compared to the total number of special resources (disregarding ocean squares that cannot contain huts either).
Same as for special resources, the right operand's value range being [0..31], there is a repeating pattern, which is highlighted below (areas with a red overlay cannot contain huts):

As for special resources, when matching with the first operand, we can see how the right operand pattern repetition also results in the repetition of the huts pattern:

1.2. Adjusting the pattern by hacking the formula
Obviously, adjusting numerical parameters in the formula will lead to different results when calculating the operands, and thus different patterns.
Understanding the formula as explained in 1.1. definitly helps in understanding and deciding how to change the parameters.
On the left side of the formulas, both the MOD 4 operations are actually coded as n & 0x3, where "&" is the binary AND operation. So it can only be changed powers of 2 (2, 4, 8, 16, 32, 64, etc.). Otherwise the '&' operation will no longer correspond to a MOD operation, but rather to something less understandable.
The multiplication by 4, as well, is actually a bitwise left-shift by 2 bits, so simple modification only allows for changing the number of bits shifted, i.e. powers of 2 as well.
On the right side, however, we are more lucky: the divisons by 4 are still done by bitwise right-shift by 2 bits, so still limited to powers of 2.
However, the multplications by 13 and 11 are done directly, so those 2 multipliers are the easiest to change. Also, there is no need to set values greater than 15, because the MOD 16 will cast them back to the [0..15] range anyway, i.e. 18 is the same as 2, for example.
The offsets of those 2 multipliers are given below:
Although the patterns obtained are still repetitive in some way, some of them seem less regular that the standard one, and could be more interesting to play or at least give new experiences in CIV games.
Hereunder I attached a HTML page that simulates the pattern for you when you change the different parameters (ZIPped because of civfanatics forum limitations):
View attachment pattern_sim.zip
Also, hereunder is a large batch of patterns that I found interesting by changing the multipliers:
||||
x multiplier|0|4|5|7
y multiplier|0|13|13|2
pattern|
 |
|
 |
|
 |
|

||||
x multiplier|7|7|8|9
y multiplier|13|14|14|10
pattern|
 |
|
 |
|
 |
|

||||
x multiplier|11|11|12|14
y multiplier|2|3|15|11
pattern|
 |
|
 |
|
 |
|

||||
x multiplier|2|2|5|6
y multiplier|3|5|14|7
pattern|
 |
|
 |
|
 |
|

In progress...
In progress...
But right after posting it, I started to wonder: in what more sophisticated/interesting ways could this routine be altered?
To investigate possibilities, I started to explore 3 different approaches:
- Adjust the original formula to change the "shape" of the well known resource/hut pattern
- Completely rewrite the routine to produce more random, unpredictable patterns
- Completely rewrite the routine to make special resources and/or huts "customizable" by having them stored in/loaded from the MAP rather than computed in real time with a formula
Hereunder, I provide more details about each approach (only 1. completed thus far).
1. Adjust existing patterns
The 2 formulae to determine whether or not a map square contains a special resource or a hut are re-stated hereunder:
Code:
[b]SPECIAL RESOURCE[/b]
Y > 1 [I]AND[/I]
Y < 48 [I]AND[/I]
(X MOD 4)*4 + (Y MOD 4) == ((X/4)*13 + (y/4)*11 + TMW) MOD 16
[b]HUT[/b]
Y > 1 [I]AND[/I]
Y < 48 [I]AND[/I]
square at (X,Y) is not a city [I]AND[/I]
square at (X,Y) is not visible by barbarians [I]AND[/I]
(X MOD 4)*4 + (Y MOD 4) == ((X/4)*13 + (y/4)*11 + TMW + 8) MOD 32The first few elements of those boolean formulae are simply checking for other external conditions (square not in poles, hut not already visited, etc).
The last operand of both formulae are the ones that control those very peculiar patterns that CIV players quickly get familiar with:

Special resource pattern

Huts pattern

1.1. In-depth pattern analysis
Before altering those formulae, let's try to make some sense out of them (if you're not interested, you can skip this part and go to 1.2. directly).
First, let's look at the left operand, which is identical for both formulae:
Code:
[B](X MOD 4)*4 + (Y MOD 4)[/B]X and Y are the coordinates of the map square. If we exclude the poles, they range, respectively, from 0 to 79 (included) and from 2 to 47 (included). The square with coordinates (0,0) is the top-left corner of the map, and from this square, the X and Y coordinates increase 1 by 1 horizontally towards the right (X) and vertically towards the bottom (Y). It can be represented as follows:

The meaning of N MOD 4 is the value of integer N modulo 4, or in other words, the remainder of the integer division of N by 4. One of the properties of the modulo operation is that it produces cyclical values when given a linear input range of integers.
Typically:
Code:
if the value of [B]N[/B] is 0 1 2 3 [I] 4 5 6 7[/I] 8 9 10 11 [I]12 13 14 15[/I] 16 17 ...
then [B]N MOD 4[/B] is 0 1 2 3 [I]0 1 2 3 [/I] 0 1 2 3 [I]0 1 2 3[/I] 0 1 ...With this property in mind, we can get the intuition that if X MOD 4 and Y MOD 4 are both cyclical, then (X MOD 4)*4 + (Y MOD 4) is also going to be cyclical, all the more that (X MOD 4) is multiplied by 4, which happens to be modulo divisor.
When computing (X MOD 4)*4 + (Y MOD 4) for all map squares (X,Y), we immediately see a cyclical pattern appear, as highlighted in blue in the grid below:

The cyclic pattern is a 4x4 area that contains values from 0 to 15, ordered from top to bottom and left to right.
In other words, the left operand divides the map in a set of identical 4x4-square areas, each area containing all values from 0 to 15.
Now, let's look at the right operands:
Code:
Special resources: [color=green][b]((X/4)*13 + (Y/4)*11 + TMW) MOD 16[/b] [/color]
Huts: [color=red][b]((X/4)*13 + (Y/4)*11 + TMW + 8) MOD 32[/b] [/color]Here again, there is a strong similarity between both formulae, the only differences being the final MOD divisor (16 vs 32) and the addition of 8 for the Hut formula.
Let's look at the identical part first: (X/4)*13 + (Y/4)*11 + TMW
Here, N/4 yields the quotient of the integer division of N by 4. When applied to a continuous range of values like 0, 1, 2, 3, 4, 5, 6, ..., this operation is guaranteed to return the same result for 4 consecutive values:
Code:
if the value of [B]N[/B] is 0 1 2 3 [I] 4 5 6 7[/I] 8 9 10 11 [I]12 13 14 15[/I] 16 17 ...
then [B]N/4[/B] is 0 0 0 0 [I]1 1 1 1 [/I] 2 2 2 2 [I]3 3 3 3[/I] 4 4 ...Again, when applied to both X and Y, we can foresee that this formula will work at a the level of 4x4-square areas:

We also see in the picture above that X/4 and Y/4 are symmetrical, and this is always an issue when trying to design a random pattern.
This is why CIV developers multiply X/4 by 13 and Y/4 by 11. The reason for choosing 11 and 13 as multipliers is that they are both prime numbers whose smallest common mulitplicant is, thus, their own product 11 x 13. Another reason is that they result in a rather nice and even pattern...
This beats symmetry because the smallest X and Y necessary for X/4*13 being equal to, and thus symmetrically exchangeable with Y/4*11, are X = 11*4 = 44 and Y = 13*4 = 52, which never happens since Y is always smaller than 52.
So this guarantees that X/4*13 + Y/4*11 always yields different results for all values of X and Y within the map.
In this part of the formula, the addition of the Terrain Master Word (TMW) brings variation in the pattern from game to game.
Looking only at the special resource formula, the final step is the MOD 16 operation, which effectively gets the value of X/4*13 + Y/4*11 + TMW within the range [0..15]:

Since we are only dealing with values between 0 and 15 though, we cannot avoid having a pattern repetition in those right operand values, as highlighted below, where all colored areas are identical:

Now, since the resulting value of both operands are within the range [0..15], there is a guaranteed single match between both operands for every 4x4 area. In other words, there is 1 and only 1 square for each 4x4-square area on the map that will make the special resource formula true:

Matching with the first operand, we can see how the right operand pattern repetition results in the repetition of the special resource pattern as well:

Now let's look a the right operand of the hut pattern formula: ((X/4)*13 + (Y/4)*11 + TMW + 8) MOD 32
Compared to the special resource formula, the addition of 8 plays only a little role, which is to shift the pattern compared to the special resrouce pattern, otherwise, without this "+8", every hut square would also be a special resource square.
The real difference lies in the 32 MOD divisor (0x1F) instead of 16 (0xF) for special resource: the MOD 32 operation will cast the right operand values for the 4x4 areas ( (X/4)*13 + (Y/4)*11 + TMW + 8 ) into the [0..31] range, instead of [0..15] for the special resource pattern.
Since the left operand values' range is only [0..15], this means that 4x4 areas for which the right operand value ranges from 16 to 31 will not contain any square for which the hut formula is true, i.e. those 4x4 areas will not contain any hut square. Those areas have a gray background in the picture below:

On average, this cuts by half the potential number of huts compared to the total number of special resources (disregarding ocean squares that cannot contain huts either).
Same as for special resources, the right operand's value range being [0..31], there is a repeating pattern, which is highlighted below (areas with a red overlay cannot contain huts):

As for special resources, when matching with the first operand, we can see how the right operand pattern repetition also results in the repetition of the huts pattern:

1.2. Adjusting the pattern by hacking the formula
Obviously, adjusting numerical parameters in the formula will lead to different results when calculating the operands, and thus different patterns.
Understanding the formula as explained in 1.1. definitly helps in understanding and deciding how to change the parameters.
On the left side of the formulas, both the MOD 4 operations are actually coded as n & 0x3, where "&" is the binary AND operation. So it can only be changed powers of 2 (2, 4, 8, 16, 32, 64, etc.). Otherwise the '&' operation will no longer correspond to a MOD operation, but rather to something less understandable.
The multiplication by 4, as well, is actually a bitwise left-shift by 2 bits, so simple modification only allows for changing the number of bits shifted, i.e. powers of 2 as well.
On the right side, however, we are more lucky: the divisons by 4 are still done by bitwise right-shift by 2 bits, so still limited to powers of 2.
However, the multplications by 13 and 11 are done directly, so those 2 multipliers are the easiest to change. Also, there is no need to set values greater than 15, because the MOD 16 will cast them back to the [0..15] range anyway, i.e. 18 is the same as 2, for example.
The offsets of those 2 multipliers are given below:
Code:
offsets for: 13 (0xD) - 11 (0xB)
EN 47401: 0x1C885 - 0x1C893Although the patterns obtained are still repetitive in some way, some of them seem less regular that the standard one, and could be more interesting to play or at least give new experiences in CIV games.
Hereunder I attached a HTML page that simulates the pattern for you when you change the different parameters (ZIPped because of civfanatics forum limitations):
View attachment pattern_sim.zip
Also, hereunder is a large batch of patterns that I found interesting by changing the multipliers:
x multiplier|0|4|5|7
y multiplier|0|13|13|2
pattern|




x multiplier|7|7|8|9
y multiplier|13|14|14|10
pattern|




x multiplier|11|11|12|14
y multiplier|2|3|15|11
pattern|




x multiplier|2|2|5|6
y multiplier|3|5|14|7
pattern|




2. Rewrite formula to be more random
In progress...
3. Rewrite formula to store special squares in MAP
In progress...