Well, thew distribution doesn't have to be exactly symmetrical, indeed. But it is always exactly symmetrical for the mean, the 68% in between +/- 1SD, 95% from -2SD to +2SD etc.
Why?
Because it is the IQ, a quotient, not a distribution of measured "Intelligences".
It is something like an overlay for test results (number of correct answers), which are surely not idealy distributed, to enable us comparing different tests.
The IQ or any comparable issue (like normal ranges for medical labratory parameters) are generated from that results, to exactly fit the Gaussian model.
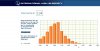
Example: You run a test with 1000 participants. The average score is 70 out of 100. Now you simply take the 34% above and the 34% below and declare them to be the average population, IQ =100. The next 13.5% in both directions are the +/- 1SD pop. In terms of 1SD= 15 on the IQ scale, this gives 85 and 115. 115 may not sound that much, but it does mean you're smarter than 84% of the group! Most test are not suitable for more than 2 or 3 SDs, and 1000 is rather few, so we're only able to filter the 2SD population out; those are always the 25 most dumb and the 25 smartest people out of a crowd of 1000. To get any further info about those guys, we'd have to compare them with a large group of equally IQs.