You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Maths quiz
- Thread starter Dell19
- Start date
Lucky
Game- and Quizmaster
- Joined
- Nov 6, 2001
- Messages
- 2,304
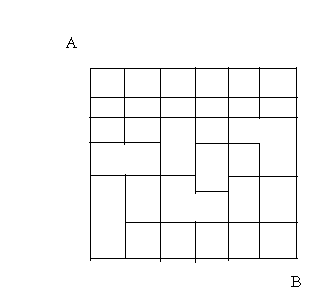
Of course it´s not. But IF I understood you rules correctly it would simply be a matter of counting. The problem is that this reduces your question to simple hard work, not thinking. There are plenty of ways in your diagramm, more than a lot of us are willing to count.


AVN
Deity
So, there is a much easier way to solve this problem.
(I also thought I had to count all the possibilities).
In that case you will teach us something valuable.

(I also thought I had to count all the possibilities).
In that case you will teach us something valuable.


- Joined
- Oct 5, 2001
- Messages
- 30,080
Right. I'll demonstrate the method on a simpler example.
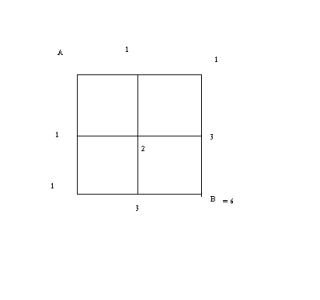
In the diagram below, basically you start at point "A" and you count the different ways to get to each of the next possible intersections. Obviously, you can either go down, or right.
Going down, there is only 1 possible way of getting to that intersection, so we write "1" there.
Going across, there is also only 1 possible way to get to the first intersection, so we write 1 there as well.
With the rule stating that you can only travel right or downwards, it is fairly obvious that there is only one possible way of getting to any of the intersections on the left-hand edge. We can write "1" by each of these. By the same logic, we can write "1" at each intersection across the top.
Now for the internal intersections. This is a simple addition problem: At each intersection, the number of ways to get to it is the sum of the number of ways to get to the intersection on the left , and the number of ways to get to the intersection above it.
There is therefore two possible ways to get to the center intersection, three ways to get to either the bottom-middle or Right-middle intersection. These can be summed to show six ways of getting to "B".
In the diagram below, basically you start at point "A" and you count the different ways to get to each of the next possible intersections. Obviously, you can either go down, or right.
Going down, there is only 1 possible way of getting to that intersection, so we write "1" there.
Going across, there is also only 1 possible way to get to the first intersection, so we write 1 there as well.
With the rule stating that you can only travel right or downwards, it is fairly obvious that there is only one possible way of getting to any of the intersections on the left-hand edge. We can write "1" by each of these. By the same logic, we can write "1" at each intersection across the top.
Now for the internal intersections. This is a simple addition problem: At each intersection, the number of ways to get to it is the sum of the number of ways to get to the intersection on the left , and the number of ways to get to the intersection above it.
There is therefore two possible ways to get to the center intersection, three ways to get to either the bottom-middle or Right-middle intersection. These can be summed to show six ways of getting to "B".
Attachments
- Joined
- Oct 5, 2001
- Messages
- 30,080
Originally posted by Lucky
Yes, easier indeed, but still a lot of work.
 It took me longer to draw the diagram than to count the different ways! (I make it 378 by the way).
It took me longer to draw the diagram than to count the different ways! (I make it 378 by the way).Anyway, next question:
Arrange the numbers 2, 4, 6, 8, 10, 12, 14, 16 and 18 into a three x three square, so that each horizontal row and vertical column add to the same number.
AVN
Deity
Ainwood,
One of the possible solutions is :
12 - 14 - 4
2 - 10 -18
16 - 6 - 8
This was easy.
One of the possible solutions is :
12 - 14 - 4
2 - 10 -18
16 - 6 - 8
This was easy.
- Joined
- Oct 5, 2001
- Messages
- 30,080
YEP!Originally posted by AVN
This was easy.
Your go
(you pipped Lucky by a few hundred trillian periods of the radiation, which correlates to the transition between both Hyperfineniveaustructures (?) of the basic state of the atom Caesium 133)

AVN
Deity
The next question is not too difficult, and it is civ3 related.
You are playing the Germans against 6 random opponents (out of 15).
How many combinations of opponents are there ?
PS : Lucky you were indeed quicker , but as you requested I take it on.

You are playing the Germans against 6 random opponents (out of 15).
How many combinations of opponents are there ?
PS : Lucky you were indeed quicker , but as you requested I take it on.


Hitro
Feistus Raclettus
That should be right, Lucky.
15 choose 6 is 5005 I think. Or we did something completely wrong as it seemed to be quite easy...
15 choose 6 is 5005 I think. Or we did something completely wrong as it seemed to be quite easy...
AVN
Deity
You are both completely right.
In general people don't like stochastics, so therefore I gave a simple problem.
But I understand that you both know a lot about it, so be prepared for my following problem

But for now it's Lucky's turn.
In general people don't like stochastics, so therefore I gave a simple problem.
But I understand that you both know a lot about it, so be prepared for my following problem


But for now it's Lucky's turn.
- Joined
- Oct 5, 2001
- Messages
- 30,080
Originally posted by Lucky
Actually I was faster! I posted at 6:46 my time, ainwood at 6:45. BUT he actually posted his answer at 6:53 my time, not earlier. My last edit was at 6:52.
I don´t mind though, go ahead, next question!

OOPS! Sorry - I looked at the order they appeared on the thread. I didn't see the post before it was edited.
Lucky
Game- and Quizmaster
- Joined
- Nov 6, 2001
- Messages
- 2,304
Now, let´s see. I don´t have time to think of a really nice one so this will have to do! 
Division of 2 complex numbers:
z1=-SQRT(3) + i
z2=-SQRT(8) + i*SQRT(8)
Calculate z3=z1/z2 ! What is the absolute value of z3 (|z|) and what is its phase (f)?
Write z3 in the cartesian and the exponential form (z=a+ib, z=|z|*e^if)!
i is the imaginary unit!
I hope the translation was correct.


Division of 2 complex numbers:
z1=-SQRT(3) + i
z2=-SQRT(8) + i*SQRT(8)
Calculate z3=z1/z2 ! What is the absolute value of z3 (|z|) and what is its phase (f)?
Write z3 in the cartesian and the exponential form (z=a+ib, z=|z|*e^if)!
i is the imaginary unit!
I hope the translation was correct.

Similar threads
- Replies
- 10
- Views
- 1K
[Extension]
Enlightenment Era for VP (4.22)
- Replies
- 72
- Views
- 9K