Physics Help

[Eiba]

I've lurked here for a while, and noted that there seem to be a good number of people who are good at math/science.

Well in my physics class today we were doing some practice problems having to do with light refraction/reflection, prisms, etc. though as it turned out there was one question that my teacher couldn't even figure out. I think I got an answer, but it's really convoluted- my teacher was unable to verify if it was right or wrong, and so I ask the forumgoers of CFC: How do you do this problem?

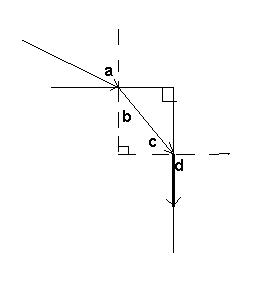
"A given monochromatic light ray, initially in air, strikes the 90 degree prism at P and is refracted there and at Q to such an extent that it just grazes the right-hand prism surface after it emerges into air at Q."


(I apologize for my poor Paint skills... hopefully you get the picture)

"Determine the index of refraction, relative to air, of the prism for this wavelength in terms of the angle of incidence (theta-sub-1), which gives rise to this situation. n = _____"

My teacher said we could assume "just grazes the surface" to mean that it's 90 degrees from the normal. Using Snell's law and some trigonometry I got two equations (writing theta-sub-1 as theta1 for simplicity) where theta-sub-2 (theta2) is the angle between the normal and the light ray at point P:

1 * sin theta1 = n * sin theta2

n * (sin 90 - theta2) = sin 90 * 1 = 1
Or (because of the way the triangle works):
n * cos theta2 = 1

I solved the second equation for n and got (1 / cos theta2) then plugged that into the first equation for:
sin theta1 = sin theta2 / cos theta2 = tan theta2

I thought that was a dead end, so mainly to fool around I tried solving for theta2:

arctan sin theta1 = theta2

Then plugging that into the first equation:

sin theta1 = n * sin arctan sin theta 1
or:
n = sin theta1/sin arctan sin theta1

And that is technically n in terms of theta1... But it's a horribly ugly answer... My physics teacher said I had a twisted mind to come up with such a thing.

Can anyone tell me where I went wrong or how to do it? Or if that's actually right?


I'll be happy to clarify if anything I wrote is unclear.

 

[Sidhe]

Laws of Refraction:

1. The ratio of sines of the angles of incidence and refraction is a constant. (Snell's Law) (The ratio is constant for a particular wavelength and a particular set of materials.)

2. The incident and refracted rays are on opposite sides of the normal at the point of incidence.

3. The incident ray, the normal, and the refracted ray are coplanar.

Snell's Law: sin i over sin R = n where n is a constant.

the constant is the ratio of the speeds of light in the two media.)

General form: sin theta 1 over sin = n2 over n1

n = n2 over n1 = v1 over v2

or, n1sintheta1 = n2sintheta2

(The absolute index of refraction for a given medium is defined as: n = c/v where c is the speed of light in a vacuum and v is the speed of light in the medium. Also, the ratio n2/n1 is called the relative index of refraction.)

I apologise I haven't studied this particular physics, but your question interested me enough to want to look at the snell equation.

This should give you the answer your looking for, it's fairly plain to see the relationship between refractive index and the angles in question from this. You can derive first principles from these equations alone. I can see you are conversant in combining equations and the law itself gives you all you need here.

It looks to me as if your trying to overcomplicate a simple equation, simply use the equations to obtain the angle of incidence. These simple equations gives you all you need to show the relationship between angle of incidence and refractive index, I'm not sure why your resorting to complicating the basic trig at all, it looks like a dead end to me. Again I apologise though if I'm misleading you, I really do know nothing about prism effects. Occams razor is always wisest though in any scientific undertaking

EDIT: interesting, if I'm in any way misleading you I'd be fascinated to know more Just remember the speed of light in a vaccuum is c, in an object it is directly proportional to the objects refractive index, which in turn is directly proportional to the angle of refraction at both n1 and n2.

 

[Eiba]

(First, a note- my picture is slightly wrong. The theta1 should be between the doted line and the light ray.)

This should give you the answer your looking for, it's fairly plain to see the relationship between refractive index and the angles in question from this. You can derive first principles from these equations alone. I can see you are conversant in combining equations and the law itself gives you all you need here.

You'd think that'd be enough, but that's what I did essentially, and it led to the mess outlined above...

It looks to me as if your trying to overcomplicate a simple equation, simply use the equations to obtain the angle of incidence. These simple equations gives you all you need to show the relationship between angle of incidence and refractive index, I'm not sure why your resorting to complicating the basic trig at all, it looks like a dead end to me.

It looked like a dead end to me too, until I tried that thing with an arctan... then it just looked silly...

But anyway, I did use that simple equation (n1 sin theta1 = n2 sin theta2), but given the relative lack of actual values to plug in I had to resort to trig to keep my additional made up variables down to one (theta2). Otherwise, I'd have to have a variable for the angle between the ray and the normal for once it's gone in, and another for the angle between the ray and the normal for when it's going out.

The second equation could read:
n * sin theta3 = 1 * sin 90
But theta3 as it is doesn't relate to the original equation at all. Only once you replace it with (sin 90 - theta2) or (cos theta2) do you get anywhere... but I'm not sure where, as this thread is evidence of...

After that I had to use trig, as I really didn’t know how to combine the equations so as to get n in terms of theta1 otherwise

Again I apologise though if I'm misleading you, I really do know nothing about prism effects.

To my knowledge there's no effect we have to take into account as "monochromatic light" was mentioned in the problem. We just have use Snell's equation and realize that the two surfaces are perpendicular to each other.

EDIT: interesting, if I'm in any way misleading you I'd be fascinated to know more Just remember the speed of light in a vaccuum is c, in an object it is directly proportional to the objects refractive index, which in turn is directly proportional to the angle of refraction at both n1 and n2.

Well considering that they're just asking for the index of refraction, I don't see that we need to do anything that directly involves c. Other than that it all appears to be sound advice... except it's basically what I already did.

I should mention, I do greatly appreciate your help.

 

[Sidhe]

Well to be honest given that your looking at n=1.00xsin(90-22.5)/sin 90=n and this gives

Correction my calculator has gone wierd on me I get

1x.9238795325/sin 90=.9239 to 4dp

the line when it extends to the end of thee triangle bisects the top of the triangle and point Q exactly so the angle must be 99-45/2 since the angle of the base of the triangle is 45 degrees 180=90+45+45

 

[sanabas]

I have a reasonably simple solution, I don't think I've stuffed up getting it. And I also apologise for my poor paint skills.

a = angle of incidence
b= angle of refraction
c = angle of incidence for refracted ray
d = angle of refraction of refracted ray = pi/4 = 90 degrees (given)
refractive index of air = 1 (close enough)
refractive index of prism = n

So Snell's law says: 1*sin (a) = n*sin(b)
And it also says: n*sin(c) = 1*sin(d) = 1*sin(pi/4) = 1

Basic trig says that sin(b)=cos(c), as we have a right angled triangle made up of the two normals and the refracted ray.

So now we have:
sin(a) = n*cos(c) (eq 1)
n*sin(c) = 1
therefore n^2*sin^2(c) = 1^2 = 1. (eq 2)

Basic trig identity says sin^2(c) + cos^2(c) = 1
So cos(c)=sqrt[1-sin^2(c)]
So n*cos(c) = sqrt[n^2 - n^2*sin^2(c)] (eq 3) (multiplied both sides by n, put n under the sqrt sign)

Sub eq 2 into eq 3, and we have:

n*cos(c) = sqrt[n^2 -1]

Sub that into eq 1, and we have:

sin(a) = sqrt[n^2 - 1]
sin^2(a) = n^2 - 1
n^2 = sin^2(a) + 1
n = sqrt [sin^2(a) + 1], and you now have the answer to the question, ad a cunning method to determine the refractive index of an unknown substance.

 

[Sidhe]

well I hope your right but that give me 1.414

Where as the original snell equation gives me something totally different?



angle of internal difraction=45 degrees

angle of incidence= 67.5 degrees

Find:

n = ???

n* sin(angle of incidence)= sin(angle of difraction)

n* sin(67.5)=sin(45)

n * -.99902418 = .8509035245

n= -.99902418/8509035245

n = -1.174071386

Which is again different from the answer above and I have forthwith used mathcad to show the answers here, hoping that my calculator will eventually give reliable information

must be GIGO

 

[Mise]

I get the same as sanabas, except I left the refractive index of air in (as per the original question), so it's n2/n1=sqrt(1+sin^2(theta1)).

 

[Sidhe]

I think the problem with the way I'm doing it i.e the given scientific method of finding n from refractive index and angle of incidence is I'm assuming numbers that probably aren't accurate because of the paint picture being mislabled and misdrawn. I will say this though if you plug those numbers you have values for into the Snell equation you get that number, but when I plug those numbers into the other equation I get something completely different where am I going wrong, because this method of finding n with only knowing the two angles(I stole it off the net from an educational web site although I derived it anyway originally from rearranging the eqation for n) is obviously wrong either that or your derived equation is obviously wrong. I'd like to know which?

n2/n1=sin(67.5)/sin(45)

1 * sin theta1 = n * sin theta2

1*sin(67.5)/sin(45)=n

or if 90 degrees I get= -1.1117

 

[Mise]

Where are you getting those angles from?

 

[Sidhe]

The imaginary line or line light would take if not difracted, bisects the triangle at half the distance from top to base, thus the angle of difraction must = 67.5 or 90-45/2. Take ruler stick it on the screen, you'll see what I mean if you draw a line through an equalateral triangle 90+45+45=180 degrees the triangle that bisects it then it will equal 22.5 degrees. since p to i is 22.5 degrees the angle of incidence is 90-22.5 degrees there is your answer.

 

[Mise]

But we're saying that the angle of incidence is arbitrary, i.e. what does the refractive index have to be for the light to travel along the edge of the prism at Q when light is incident at P at some angle theta.

 

[Sidhe]

Yes but if I plug my number for theta into your equation I get an answer other than the answer snells law gives, in other words, your equation doesn't produce anything like the actual results of Snells equation, therefore Either Snells equation is wrong or yours is.

Try it for yourself you have angle of incidence as 67.5, what does that give you, now do Snells equation what does that give you?

Surely the answers should be the same? or is that an irelevance?

As far as I can see I can't fault your maths at all. What I can fault is the "real world" evidence which it seems to contradict.

I get the same as sanabas, except I left the refractive index of air in (as per the original question), so it's n2/n1=sqrt(1+sin^2(theta1)).

Specifically this if theta 1 is 67.5 which it is you can see that from basic trig. So I expect the answer to snells law

ie n=n2/n1=1*sin(theta sub 1)/Sin(theta sub 2) to equal n2/n1=sqrt(1+sin^2(theta sub 1))

 

[Mise]

I honestly don't know what you're talking about, sorry. I think you're misunderstanding the question and/or what snell's law is. In the prism, the light refracts twice, once at P and once at Q, so snells law needs to be applied to both cases, with the angle of refraction for P being related geometricaly to the angle of incidence for Q.

 

[Sidhe]

OK I obviously am missing something what I want to know is if I take

i=67.5 and r=90

And I plug that into snells to find the refractive index will it produce the same refractive index as your equation?

What I want to know is how it works, and why when I follow the web sites method of finding n or n2/n1 or v2/v1 or c/v or whatever I get a completely different number from when I follow your method? Show me the working of using snells then your equation, both should produce the same answer yes?

Your catch all equation should work for all values of i and r lim 0-->90 yes?

 

[Mise]

Sidhe, as I said, you need to understand the problem better. The angle of incidence you call i=67.5 is NOT the same as what I call theta1 -- it is what sanabas calls "c". For convention lets just use sanabas's notations:

1. Use snell's law at Q to show that n.sin(c)=sin(d) (where we have assumed that the refractive index outside the prism is 1 and inside is "n") ...... eqn 1

2. Realise that sin(c) is equal to cos(b) by trigonometry, and sin(d) = 1; => n.cos(b)=1 ............ eqn 2

3. Apply snell's law to refraction at P to show that sin(a)=n.sin(b) ......... eqn 3

4. Square eqn 2 and 3 up:
n^2.cos^2(b) = 1 ..................... eqn 4a
sin^2(a) = n^2.sin^2(b) ............ eqn 4b

5. Add 4a to 4b and recognise that sin^2(b) + cos^2(b) = 1:
n^2 = 1 + sin^2(a) ................ eqn 5

6. Take the square root of that to get n in terms of angle of incidence a:
n = sqrt( 1 + sin^2(a) )

-----------------

Can you explain to me what exactly you are doing? I'm still not sure. There should be four angles, not two, for a start.

 

[sanabas]

Well, I did make one stuff up in my answer. I wrote 90 degrees as pi/4. Twice. Complete brainfart there, but just a typo that doesn't change anything.

well I hope your right but that give me 1.414

Where as the original snell equation gives me something totally different?

I think I have spotted your mistake in this working, and I agree with Mise, I can't understand your posts after this one.

angle of internal difraction=45 degrees

So on my diagram, b & c = 45 degrees.

angle of incidence= 67.5 degrees

And a = 67.5 degrees. There's your first mistake. You can only set 1 of those angles yourself. d is set at 90, as soon as you set a, b, or c, you have enough information to find the refractive index and all the other angles.

Find:

n = ???

n* sin(angle of incidence)= sin(angle of difraction)

n is in the wrong spot. This is the equation for the ray leaving the prism, not for the ray entering the prism. For a ray to bend towards the normal, as it does if the angle of incidence is 67.5, refraction is 45, it must be entering a slower medium. According to what you've written, it is entering air/vacuum, as n(refraction) is 1. Which means n(incidence) is less than 1, light moves quicker than it does in a vacuum, and you've redefined the laws of physics.

n* sin(67.5)=sin(45)

n * -.99902418 = .8509035245

n= -.99902418/8509035245

n = -1.174071386

Nevermind that n is in the wrong place. If you are working in degrees, set your smegging calculator to degrees, not radians!

67.5 degrees is an acute angle, sin of that being negative immediately says something is wrong. Sin 45 you should know as 1/sqrt 2 = 0.707. Your answers above are perfectly correct if the angles are 67.5 & 45 radians.

Which is again different from the answer above and I have forthwith used mathcad to show the answers here, hoping that my calculator will eventually give reliable information

Your calculator will give reliable info as soon as you plug in reliable data.

Going off my diagram, there are two places to apply snell's law. First when the ray enters the prism, second when it leaves. Using the values you're trying to, the first equation gives:

sin(67.5) = n * sin(45)
n = sin(67.5)/sin(45)
n = 1.3 (to 2 sig figs)

For the second equation, we have:

n * sin 45 = sin 90
n = sin 90/sin 45
n = 1/(1/sqrt2)
n = sqrt 2
n = 1.4 (to 2 sig figs)

must be GIGO

What is GIGO?

Try it for yourself you have angle of incidence as 67.5, what does that give you, now do Snells equation what does that give you?

Surely the answers should be the same? or is that an irelevance?

The answers for n will be the same if the diagram is accurate. I will work through the equation if the initial angle of incidence is 67.5 degrees.

So n = sqrt (sin^2(67.5) + 1)
n = sqrt (0.92^2 + 1)
n = 1.361

Now to apply snell's and see what we get on entering the prism:

1*sin(67.5) = 1.361 * sin (b) (b being initial angle of refraction)
sin (b) = sin (67.5)/1.361
sin (b) = 0.679
b = 42.73 degrees

Now to apply snell's when leaving the prism:

c = 90 - 42.73 = 47.27 degrees. We now know the angles of incidence and refraction, and the refractive index of both substances, so both sides of this equation should be equal, if they're not we have made a mistake somewhere.

1.361 * sin (47.27) = 1 * sin (90)
1.361 * 0.735 = 1 * 1
1 = 1 (Actually it's 1.000335 if you've rounded as you went. I didn't, I kept exact values stored in my calculator as I went, and it is exactly 1.)

And I plug that into snells to find the refractive index will it produce the same refractive index as your equation?

What I want to know is how it works, and why when I follow the web sites method of finding n or n2/n1 or v2/v1 or c/v or whatever I get a completely different number from when I follow your method? Show me the working of using snells then your equation, both should produce the same answer yes?

Your catch all equation should work for all values of i and r lim 0-->90 yes?

Yes to all, as shown above. Except for the last one. It will work for all values of i, 0<i<90. r is irrelevant, r gets worked out afterwards once you've found n.

As for the bolded question, the answer is RADIANS! I can sympathise, in year 12 I did an entire vectors test with my calculator set to radians, but answering questions that were asked in degrees. I only noticed after finishing every question that all my answers were between 0 & pi. That made for some really frantic rewriting and reevaluating.

I get the same as sanabas, except I left the refractive index of air in (as per the original question), so it's n2/n1=sqrt(1+sin^2(theta1)).

Yep. I was just being lazy. I think the question said find the index relative to air, so I didn't bother with writing n2/n1 over and over.

 

[Sidhe]

Well, I did make one stuff up in my answer. I wrote 90 degrees as pi/4. Twice. Complete brainfart there, but just a typo that doesn't change anything.




I think I have spotted your mistake in this working, and I agree with Mise, I can't understand your posts after this one.





So on my diagram, b & c = 45 degrees.



And a = 67.5 degrees. There's your first mistake. You can only set 1 of those angles yourself. d is set at 90, as soon as you set a, b, or c, you have enough information to find the refractive index and all the other angles.



n is in the wrong spot. This is the equation for the ray leaving the prism, not for the ray entering the prism. For a ray to bend towards the normal, as it does if the angle of incidence is 67.5, refraction is 45, it must be entering a slower medium. According to what you've written, it is entering air/vacuum, as n(refraction) is 1. Which means n(incidence) is less than 1, light moves quicker than it does in a vacuum, and you've redefined the laws of physics.



Nevermind that n is in the wrong place. If you are working in degrees, set your smegging calculator to degrees, not radians!

67.5 degrees is an acute angle, sin of that being negative immediately says something is wrong. Sin 45 you should know as 1/sqrt 2 = 0.707. Your answers above are perfectly correct if the angles are 67.5 & 45 radians.




Your calculator will give reliable info as soon as you plug in reliable data.

Going off my diagram, there are two places to apply snell's law. First when the ray enters the prism, second when it leaves. Using the values you're trying to, the first equation gives:

sin(67.5) = n * sin(45)
n = sin(67.5)/sin(45)
n = 1.3 (to 2 sig figs)

For the second equation, we have:

n * sin 45 = sin 90
n = sin 90/sin 45
n = 1/(1/sqrt2)
n = sqrt 2
n = 1.4 (to 2 sig figs)



What is GIGO?



The answers for n will be the same if the diagram is accurate. I will work through the equation if the initial angle of incidence is 67.5 degrees.

So n = sqrt (sin^2(67.5) + 1)
n = sqrt (0.92^2 + 1)
n = 1.361

Now to apply snell's and see what we get on entering the prism:

1*sin(67.5) = 1.361 * sin (b) (b being initial angle of refraction)
sin (b) = sin (67.5)/1.361
sin (b) = 0.679
b = 42.73 degrees

Now to apply snell's when leaving the prism:

c = 90 - 42.73 = 47.27 degrees. We now know the angles of incidence and refraction, and the refractive index of both substances, so both sides of this equation should be equal, if they're not we have made a mistake somewhere.

1.361 * sin (47.27) = 1 * sin (90)
1.361 * 0.735 = 1 * 1
1 = 1 (Actually it's 1.000335 if you've rounded as you went. I didn't, I kept exact values stored in my calculator as I went, and it is exactly 1.)



Yes to all, as shown above. Except for the last one. It will work for all values of i, 0<i<90. r is irrelevant, r gets worked out afterwards once you've found n.

As for the bolded question, the answer is RADIANS! I can sympathise, in year 12 I did an entire vectors test with my calculator set to radians, but answering questions that were asked in degrees. I only noticed after finishing every question that all my answers were between 0 & pi. That made for some really frantic rewriting and reevaluating.



Yep. I was just being lazy. I think the question said find the index relative to air, so I didn't bother with writing n2/n1 over and over.

GIGO is garbage in garbage out(very apt: in computing it means if you feed crap in you get crap out) and thanks for the pointers, I've got this new graphics calculator and I think it's smarter than I am

The diagram is the problem if you extend the light ray it clearly shows the angle of incidence to be 67.5 as it bisects the triangle exactly at the half point thus my misaprehension in that I was looking in the wrong place and using the wrong tools oops, I did mention of course that the diagram was in error but only it seems in where things are placed. Very valuable to me this thread, I haven't studied anything to do with degrees yet and I guess I'm hugely ignorant, not having been in full time education for 15 years. Thanks for your time

 

[sanabas]

GIGO is garbage in garbage out(very apt: in computing it means if you feed crap in you get crap out) and thanks for the pointers, I've got this new graphics calculator and I think it's smarter than I am

No worries. I'll learn to use a graphics calc one day, my tutoring students all use them, I keep pinching them and making them use pen, paper & brains.

The diagram is the problem if you extend the light ray it clearly shows the angle of incidence to be 67.5 as it bisects the triangle exactly at the half point thus my misaprehension in that I was looking in the wrong place and using the wrong tools oops, I did mention of course that the diagram was in error but only it seems in where things are placed.

Diagrams are hardly ever the problem, diagrams are only meant to be to scale and perfectly accurate in architecture. In maths, a diagram is just a quick sketch to show what you're talking about.

Very valuable to me this thread, I haven't studied anything to do with degrees yet and I guess I'm hugely ignorant, not having been in full time education for 15 years. Thanks for your time

No worries. You haven't studied anything with degrees yet? You mean radians? Degrees are what you learn in primary school, radians usually only appear in late high school, when you start doing more trig.