What's the big deal about Hexagonal map grids?

[Belarin]

Both hex grids and square grids (and all discrete grids for that matter) have the property that there is some optimal direction of travel, the direction in which one can move the fastest. On a square grid the optimal directions are the 4 diagonals. On a hex grid, the optimal directions are the perpendiculars to the 6 edges.

Consider the distance that is moved in a single move in one of these optimal directions. We'll call that distance d. If we then wanted to move some very large distance, l, in a direction which happened to be one of our optimal directions, then we could do so in l/d turns.

Suppose instead that we wish to move in a different non-optimal direction. The difference in angle between this new direction and the nearest optimal direction forms some angle, theta.

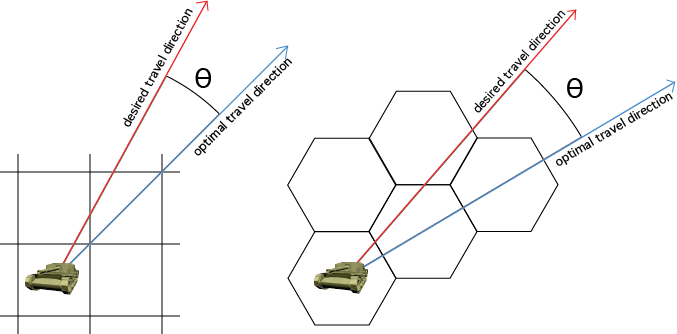
In order to move the same distance, l, in the new direction, one must expend more moves. We can think of movement along the optimal direction as being perfectly efficient in that it takes 1.0 * l/d turns to travel l distance, whereas movement in other directions takes E * l/d turns with E being some number greater than 1.0. E represents the inefficiency of moving in the new direction.

This efficiency is a function of the angle theta. When theta = 0, we are moving directly along one of the optimal directions, so E = 1.0. The inefficiency climbs to its maximum value when the required direction lies directly between two optimal directions. This graph shows the proportional number of moves require to travel a set distance as theta varies.

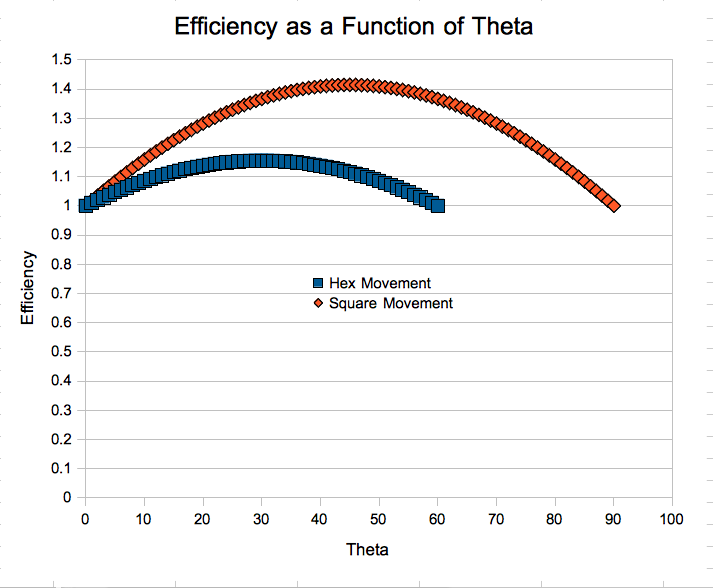
So the difference between hex and square grids is really just one of degree (at least in the case of large open areas when journeys on the square grid can always be made with a combination of diagonal moves). In a square grid, cost of moving can be up to 41% higher depending on the direction of travel, whereas on the hex grid the least efficient directions only cost 15% more.

While neither grid can really be said to be perfectly realistic, the greater uniformity of the hex grid is why it is generally used for wargames.

 

[Balderstrom]

Personally, I don't care for hexagonal grids for movement nor map layouts. The whole movement "distance issue" is moot to me, as it has an inherent assumption that the unit moves from the exact center of a hex (or square) tile to the exact center of an adjacent tile.

With hex tiles you are unable to move due east or west in a single move, no such tile exists in that location. What I do know is 1UPT combined with counting the overland map as the "strategic combat map" does not work on many levels.

Movement in CIV could easily be converted to a real-distance calculation, and leave the grid for purposes of resource and improvement allocation only.

Note: Many games don't use grids, e.g. RISK, Warlords (1, 2, 3). In Risk movement is adjacent countries only, and in Warlords movement is equated by how far you are really moving ( internally it might do grid calculations, but the overland movement displayed is the distance red-arrow ).

(OT) As far as combat is concerned:
What might work in Civ4 would be to limit squares to 6-9 units. And possibly allow combining similar units, which may or may not include a STR adjustment, but would primarily just increase the total HPs of that unit. Not sure what the disadvantage of combining units would be, beyond the obvious of decreasing the max-hps of the combined unit as each 'piece' dies.

 

[Dhoomstriker]

On a square grid the optimal directions are the 4 diagonals. On a hex grid, the optimal directions are the perpendiculars to the 6 edges.

Consider the distance that is moved in a single move in one of these optimal directions. We'll call that distance d. If we then wanted to move some very large distance, l, in a direction which happened to be one of our optimal directions, then we could do so in l/d turns.

... (at least in the case of large open areas when journeys on the square grid can always be made with a combination of diagonal moves)

Very neat math, thanks for sharing!

One immediate problem that I see with this analysis is that it appears to be using a square grid's movement capabilities against itself.

For example, we have defined "optimal" movement as being along the diagonal. I'm not sure that doing so is really a fair approach.


Assumptions
Let's assume that we have a large, open, unrestricted area to move in (no Peaks or Ice to block us, no water bodies, etc), as you were mentioning. Also, let's assume that we have already explored the map and therefore we are not interested in revealing the fog of war.


"3N + 3E" Example
Let's say that our desired direction of travel is due east 6 squares. Based on the claim made about using diagonals, we would NOT travel the intuitive 6 consecutive movements of "1E." Instead, we would move some combination of 3 movements NE and 3 movements SE.

Intuitively, one would draw a straight line from one's point of original to one's destination and do one's best to follow it. In this case, that would mean moving your unit 6 squares east.

It just so happens that by using only diagonal movements, we can get there in 6 moves, as well, so this direction on your graph is represented as a "perfect case."

But what happens if we need to move 7 squares east? The way I understand it, we have just deviated from "the perfect case," since we can make 3 NE movements, 3 SE movements, but must make one "inefficient" 1E movement. If I understand how the values for the graph were generated, then we will end up with "inefficiency" in our movement.


Proposed Redefinition of Efficient Movement
I propose a redefinition of efficiency for the square grid. I suggest that moving 7 squares east IS efficient in terms of the grid's model. Further, I suggest that the optimal movement distance be based on the amount of "real" distance that can be travelled in either a horizontal or a vertical direction.

As has been discussed, one can GAIN efficiency by moving in a diagonal motion. However, one shouldn't start off by defining this gain as a REQUIRED movement--we should instead see it as a benefit of the square grid system.


"3N + 3E" Example Again
So, let's return to the 3N + 3E example. We could move 1N 3 times and then 1E 3 times, travelling a "distance" represented by the length (or equally the width) of any square in the grid times 6. However, this movement pattern is inefficient and I agree that it is not the movement pattern that should get plotted on your graph.

However, I WOULD argue that, as was mentioned, the distance that is required to be travelled in this example invokes the Pythagorus theorem, or x^2 + y^2 = z^2. Let's arbitrarily assume, without any loss of generality, that the length and width of a square equals a value of "1." In this case, the distance that we need to travel is going to be the square root of (3^2 + 3^2) = sqrt (9 + 9) = sqrt (18) = roughly 4.24.

Moving 6 squares: 3 times 1E and 3 times 1N is definitely inefficient, since 6 moves is much greater than the required 4.24 moves. However, moving there NE three times is EXTRA efficient, since 3 moves is far more efficient than the expected required 4.24 moves.

In your diagram, one could graph this case as an INVERSE value, in that efficiency goes below a value of 1. However, I would simply define a case where we managed to travel a distance of X (in this case X = 4.24) in X or less moves (3 is less than X, while 6 would have been more than X), then we can set the efficiency to a value of 1.


Not Requiring Every Unit to be Superman
In this way, we are displaying the true power of the grid to be able to "cheat reality" and go further than normal by using a diagonal path.

The way that the graph currently defines things is that we must all be Supermen and are REQUIRED to "cheat reality" at every move. Where we fail to "cheat reality," we are deemed to be "inefficient." Somehow, this approach doesn't ring all that fairly in my books.

In a square grid, cost of moving can be up to 41% higher depending on the direction of travel...

Essentially, it looks like all that we are saying is that moving diagonally instead of purely horizontally and vertically, can gain us up to 41% efficiency in movement. However, the graph presents the inverse relationship, by saying that we are punished for every "regular," non-diagonal movement. We are in fact using the square grid's inherrent "better than normal" diagonal movements against itself.

Let's look back to our "3N + 3E" example to see. Moving purely horizontally and vertically takes 6 moves. The distance required to be travelled is 4.24. (6 / 4.24) = 1.415... if we round down instead of up, is that perhaps how we got the 41% value?


Are "In Between" Values Plotted on the Graph?
Now, don't get me wrong. I'm very intersted on the math on this subject.


For example, I am still curious how one defines the set of distances to be used. For example, does a distance of "6.5" squares east get plotted on the graph or only exactly 6 squares east? What about 6.1 squares east?

If we do examine values of "in between" distances, such that "arriving" in a square would allow us to arrive at this location, how is this value treated on the graph? For example, if we are required to move a distance equal to 6.1 squares to the east, and we move 7 squares east (which would be following my definition of efficient movement) or 3 squares NE, 3 squares SE, and 1 square E (which would be your graph's definition of efficient), what value would we plot of the graph?


Some Possible Answers to the Above Question
1. Maybe we we would plot an identical value on the graph as if we were required to move exactly 7 squares east

2. Maybe we are treating a required movement of "6.1 east" as being extremely inefficient, since we had to use a "full" movement point to travel only 0.1 of the distance

3. Perhaps we are instead defining travel as being from the centre of one square or hex to the centre of any other square or hex on the grid, since, reality aside, we can only really have a particular square or hex in mind as our destination? I think that this latter approach would probably make the most sense, in that an "in between" value is not really possible, since we cannot move a "partial square" or a "partial hex" in distance

So, which is it?

 

[Belarin]

Good thoughts Dhoomstriker. I agree with a lot of what you said.

Efficiency vs. Inefficiency

One could certainly view the cardinal directions (N, S, E, and W) as defining the normal movement speed in a square grid, and then viewing the diagonals as giving faster movement. Then, just as you mentioned, the relationship would be the inverse of what I showed. Instead of needing 41% more turns to move the same distance when moving E instead of NE, one travels 41% farther in the same number of turns when moving NE instead of E. In essence, these are two alternative ways of looking at the same thing.

What I was trying to bring to light is the inconsistency that people often use when viewing hex movement vs. square movement. Both forms have a fast direction and a slow direction, but to be consistent we need to either consider both forms by their fast speed and an efficiency loss in other directions, or by their slow speed and an efficiency gain. I think that the problem is that, since the perpendicular to the edges is the slow direction on squares and the fast direction on hexes, people tend to look at diagonal movement on squares as a gain, and movement in corner directions in hexes as a loss.

This viewpoint obscures the level of similarity, and makes the forms harder to compare. All I'm trying to show is that, really, both forms are quite similar. And we can give a quantitative comparison of how much variance occurs in directional movement in each case.

Notes on the Math (And your 3 Questions)

What I am trying to compare is the euclidean distance between two points to the number of turns required to traverse between them. Certainly, choices of certain distances lead to varied results like you mentioned with the 6.1E example. The number of moves taken of each type must always be integers, and certain distance/direction pairs don't lend themselves to this.

Things smooth themselves out over large distances, however. Spending an extra move to move 160.1E instead of 160E is an insignificant difference. Thus, while this analysis is very accurate for travel over longer distances, certain specific examples of short paths can very due to the discreet move length effect.

Note that your 7E example is basically exactly the same. On the large scale, it makes sense to ignore the possibility of square moves since almost everything that can be accomplished with them can be done with just diagonal moves. I say almost, because any combination of diagonal moves will always keep us on squares of the same color (to borrow the chess analogy). Thus 7E is a bad distance since the best we can do with only diagonal moves would be to travel 4NE and 4SE, overshooting the specified distance by one. Once again, this is an important difference in the small scale, but insignificant if we compare the difference between moving 161E or 162E.

Basically, in order to parametrize the efficiency with a single argument (the angle), I have to ignore discreet distance effects (which becomes more and more accurate as the distance tends to infinity). However, Civ games are composed of many instances of moving units over short distances, so these effects are not altogether unimportant. Investigating them in a comprehensive manner (as in plotting the speed of travel between any particular square and any other particular square), however, is beyond what I'm willing to do at the moment.

 

[yturk39]

For combat & seige fans, I noticed this, too:

Surrounding a city (or army) with units and attacking from all directions on a HEX map is much easier; it only requires you to occupy SIX surrounding tiles, versus EIGHT. Those of you liking the so-called reality-based movement of HEX grids might have second thoughts after a few good ambushes.

 

[Jolly Rogerer]

In terms of gaming there are two potential issues:

1) Square grids allow the choice of 4 discreet short moves and 4 discreet long moves per pulse , while hex grids allow the choice of 6 discreet equidistant moves per pulse. Assuming that the game doesn't charge more movement points for the diagonal moves, this makes diagonal movement cheaper in terms of movement points to distance.

2) In games with square grids where Zones of Control are in effect, diagonal adjacency is significantly less inhibiting than cardinal adjacency. To be exact a unit adjacent diagonally exerts a ZoC in two tiles (excepting those already inhabited) while a unit which is adjacent in a cardinal direction exerts a ZoC in 4 tiles. Hexes perform identically on all six sides. Because of the lesser number of sides a unit can be completely surrounded by enemy ZoCs by only two units properly placed on a hex grid, while it takes three units to achieve this on a square grid.

I tend to prefer hexes for their regularity, but that's just my opinion.

 

[Dhoomstriker]

Taking an Average?

Then, just as you mentioned, the relationship would be the inverse of what I showed. Instead of needing 41% more turns to move the same distance when moving E instead of NE, one travels 41% farther in the same number of turns when moving NE instead of E. In essence, these are two alternative ways of looking at the same thing.

So, then, is it fair to really compare against a hexagon grid at all, where we have two different values of distance that we can move in the square grid, while in the hexagon grid, we only have one value of distance that we can move?

Should we consider looking at the problem with some sort of an average? Instead of separately looking at the distance when moving horizontally or vertically versus when moving diagonally, should we average the two values? Would doing so produce any sort of useful result?


Instead of Charting all Values, maybe we should just look at some reasonably-well-comparable cases?

What I was trying to bring to light is the inconsistency that people often use when viewing hex movement vs. square movement. Both forms have a fast direction and a slow direction, but to be consistent we need to either consider both forms by their fast speed and an efficiency loss in other directions, or by their slow speed and an efficiency gain. I think that the problem is that, since the perpendicular to the edges is the slow direction on squares and the fast direction on hexes, people tend to look at diagonal movement on squares as a gain, and movement in corner directions in hexes as a loss.

Then maybe, instead of plotting all values, we should look at a few representative cases and figure out some efficiency values for them?

Certain "interesting" cases immediately spring to mind:
i. moving straight south, since a hex grid can accomplish this movement relatively efficiently. On a square grid, it depends upon whether you define "1S" as being efficient or inefficient, and the distinction doesn't matter if you move an even number of squares south

ii. moving straight east, since we are then moving an "extra amount" of distance, in that we must move SE and NE just to get to two hex "columns" over to the east. For the square grid, the result would be the same as the "moving south" case

iii. moving diagonally, since the square grid seems to have maximum efficiency no matter how you define efficiency, while a hex grid doesn't do all that well when trying to move on a 45 degree angle (or as close as you can get to it)

iv. moving in a single direction on a hex grid, such as continually NE, until such a distance would "overlap" with a corresponding distance and angle on a square grid (or as close as you can get to it), since the hex grid would have maximum efficiency and the square grid... well... I'd have to see the example but since it's unlikely to align to a diagonal path, given your definition of efficiency, we'd certainly fall short of being efficient... but to what degree would be interesting to know


Maybe remove or discount all invalid values, if you aren't already doing so?

Certainly, choices of certain distances lead to varied results like you mentioned with the 6.1E example. The number of moves taken of each type must always be integers, and certain distance/direction pairs don't lend themselves to this.

Would it be easy enough to remove all invalid destinations from a graph, or would doing so actually be a very hard result to achieve? Specifically, if the angle and distance do not actually "end" at the centre of a different hex or square, then discount them from the grid, as they are not possible results... does the graph do so or not? If it does not, how easy would it be to get rid of these "impossible" values from the graph?


Removing Results that are "bad" due to using only one direction type of travel (only diagonal instead of also horizontal/vertical)?

Note that your 7E example is basically exactly the same. On the large scale, it makes sense to ignore the possibility of square moves since almost everything that can be accomplished with them can be done with just diagonal moves. I say almost, because any combination of diagonal moves will always keep us on squares of the same color (to borrow the chess analogy). Thus 7E is a bad distance since the best we can do with only diagonal moves would be to travel 4NE and 4SE, overshooting the specified distance by one.

Whoa, so you're telling me that the graph cannot differentiate between diagonal and horizontal/vertical moves? Wouldn't this fact make the inefficiency values be incorrect?

i.e. I would expect that 7E means making 6 "efficient" diagonal moves and 1 "inefficient" horizontal move.

However, what you're describing sounds like we will make 6 "efficient" diagonal moves, then will make an additional "efficient" diagonal move but will have overshot the required distance to be travelled, and then we add yet another full diagonal move on top of it.

Forgive me, but this example sounds to be so "bad" that it doesn't even seem fair to include it in the graph at all.


Diagonal versus Horizontal + Vertical
Okay, so if I understood things, the graph does not allow for non-diagonal movement for a square grid.

As we saw with the 7E example, we can get some "bad" results... and you can handle them however you want, such as not even including such examples in the results.

Still, I question the fairness in comparing systems if one is only going to use diagonal movement for a square grid but can use both diagonal and horizontal/vertical movement for the hex grid.

Would it not be fair for the hex grid to only be able to make movements NE, SE, SW, and NW, just like we are a limiting the valid movement types for the square grid?

As we saw with the square grid, one can move 6E by moving 3NE and 3SE. The same can be said of a hex grid, assuming that we count six "columns" in a hex grid as being equivalent to "meaning" 6E.

So, one would think that it would be "fair" for the hex grid to have to do the same thing when moving north of south, since the square grid apparently has to do so, too, with its limitation on using only diagonal movements.

So, 6S would then be a series of SE and SW movements for either grid. Of course, we'd be building some inefficiency into the results for the hex grid, since the square grid would only require 3 SE and 3 SW movements, while the hex grid would require 6 SE and 6 SW movements just to travel 6 squares south. But that's the point, really. If we're going to discount some possible movement from one grid type, at the cost of possible efficiency in the numbers, it seems only fair to do the same for the other grid type... and I think that we'd get some pretty yucky results in the hexagon grid for the worst cases (moving north and south) that actually would make the hexagon grid look worse in the chart than the square grid, would we not?

 

[Belarin]

Whoa, so you're telling me that the graph cannot differentiate between diagonal and horizontal/vertical moves? Wouldn't this fact make the inefficiency values be incorrect?

i.e. I would expect that 7E means making 6 "efficient" diagonal moves and 1 "inefficient" horizontal move.

However, what you're describing sounds like we will make 6 "efficient" diagonal moves, then will make an additional "efficient" diagonal move but will have overshot the required distance to be travelled, and then we add yet another full diagonal move on top of it.

Forgive me, but this example sounds to be so "bad" that it doesn't even seem fair to include it in the graph at all.

You are misunderstanding me here. I'm discussing path efficiency, which depends on the number of moves taken and the eucidean distance travelled. It does not depend on the types of moves used (except insofar as that effects how many moves are needed).

Moving 6E via 6 straight moves or 3NE + 3SE doesn't change the efficiency one bit. Both paths take the traveller to the same spot, and both do so in 6 turns.


Consider the following: In a wide open square grid, if there exists some path from square A to B using n moves in all 8 directions (N, E, S, W, NE, SE, NW, and SW), then there also exists a path using n or fewer diagonal moves which either goes from A to B or to a square next to B.

If we are considering large distances, then we don't really care whether we end up on B or adjacent to it. Therefore, in the limit as the distance goes to infinity, we can move from A to B just as quickly using diagonal moves only as using moves in all 8 directions. For this reason, square moves are irrelevant when calculating how long it takes to travel from A to B. That's all I was saying.

So, then, is it fair to really compare against a hexagon grid at all, where we have two different values of distance that we can move in the square grid, while in the hexagon grid, we only have one value of distance that we can move?

This is exactly right, and it is the complication that I've been working around. As I discussed in the above paragraph, allowing the shorter square moves doesn't change the calculations, so it is easiest to just discount them, assuming that we always move the longer distance but also that we always move on diagonals.

 

[Belarin]

Surrounding a city (or army) with units and attacking from all directions on a HEX map is much easier; it only requires you to occupy SIX surrounding tiles, versus EIGHT. Those of you liking the so-called reality-based movement of HEX grids might have second thoughts after a few good ambushes.

2) In games with square grids where Zones of Control are in effect, diagonal adjacency is significantly less inhibiting than cardinal adjacency. To be exact a unit adjacent diagonally exerts a ZoC in two tiles (excepting those already inhabited) while a unit which is adjacent in a cardinal direction exerts a ZoC in 4 tiles. Hexes perform identically on all six sides. Because of the lesser number of sides a unit can be completely surrounded by enemy ZoCs by only two units properly placed on a hex grid, while it takes three units to achieve this on a square grid.

Excellent points.

 

[Nicol.Bolas]

in hexagonal it´s really hard to go west or east..... it´s extremely annoying to move all troops 1 by 1 to west pr east....... and you wanna be going west or east all the time

square grid can be fixed by banning diagonal moves. there: fixed

 

[Iranon]

That's not fixed at all, in fact it's worse. Diagonal movement should require 1.41 moves if you want to model distances accurately, taking 2 is worse than taking 1.

 

[ParadigmShifter]

Well both are metrics.

Orthogonal only movement is the L¹ norm, while diagonal same distance as orthogonal is the L-infinity norm.

http://en.wikipedia.org/wiki/Lp_space

 

[Dhoomstriker]

Consider the following: In a wide open square grid, if there exists some path from square A to B using n moves in all 8 directions (N, E, S, W, NE, SE, NW, and SW), then there also exists a path using n or fewer diagonal moves which either goes from A to B or to a square next to B.

If we are considering large distances, then we don't really care whether we end up on B or adjacent to it. Therefore, in the limit as the distance goes to infinity, we can move from A to B just as quickly using diagonal moves only as using moves in all 8 directions. For this reason, square moves are irrelevant when calculating how long it takes to travel from A to B. That's all I was saying.

Okay, that's certainly one way of looking at the problem. What still leaves me hanging is wondering what you DO about arriving adjacent to B.

Back to the 7E example, would moving 3 NE and 4 SE "count" as being adjacent to B, since we'd end up 1S of where we wanted to be? If yes, we used 7 moves to get to a location 7 squares away, which sounds like it would get an efficiency rating of "1," right?

However, you mentioned earlier that we'd need to make an additional NE movement, so that we end up further east of B. We'd still be adjacent to 7E, but we'd be one east of there, instead of one south of there (or, without loss of generality, one north of there). However, we'd no longer have a value of "1" for efficiency, since we had to take an extra move.

So, does being adjacent to a square only "count" if you are adjacent after having gone PAST the square?

Also, how do you calculate the efficiency value when 8 moves are required to get to a distance 7 squares away? Is it just a straight-up division of 8 / 7?

 

[TheBlackHole]

Allowing movement through diagonals in square-based games open up some very strange situations. The classical example (brought up already) is a unit passing through two units on the diagonal.

For example,
OX
X_

where "X" are your soldiers and "O" is the enemy. The enemy can cross diagonally through unhindered. Games usually address this by just say "okay well, there's a ZoC, so we'll just not allow that kind of move."

OK, but a similar situation occurs when you have
LS
SL

where "L" is a land tile and "S" is a sea tile.
So what exactly is the composition of the center point? Is it a land bridge or a canal? After all, you can cross from "S" to "S" (thus making it a canal) but you can ALSO cross from "L" to "L" (thus making it a land bridge). So what IS it?

 

[ParadigmShifter]

You can't cross from S to S like that in civ IV...

 

[karadoc]

Since you guys are all talking about geometry and distances and metrics etc, I'd like to just point out again that the real planet earth is spherical. So realistically, the circumference of the globe should get shorter when further from the equator. What this mean for civ is that apparently the cost of moving a particular physical distance not only depends on which direction you go, but also where you are on the planet... east-west movement is relatively more expensive close to the equator (in civ, not in real life)

I'm just trying to highlight the fact that the whole system is a pretty crude approximation anyway; even more so if you take into account the number of years it takes to move a couple of square according to the game clock. In my opinion, being geometrically realistic is a very low priority for Civ games. Being a factor of sqrt(2) out in the cost of diagonal movement is really a non-issue. In my opinion, the more important issues related to the hex vs square debate are how many units it takes to block someone, and easy it is to understand/play the game.

 

[Saarud]

In real life there is only one optimal route from place A to B. If we have two places of interest A and B. And B is directly 90 degrees (east) of A the optimal route is to go in 90 degress. If you by chance want to take the 45 degree (northeast) and then sway back to 135 degrees (southeast) after you travel half the distance (south east) you will travel 50% longer distance. Take a map and an overlay of both hexes and squares and you see that using hexes you get a fair distants in number of hexes compared to reallife while you won't get that using squares (unless you go directly in 0 degress, 90 degress, 180 degrees or 270 degress)

That's why I don't like squares the way Cvilization 4 presents them. If Civilization 4 would be upgraded and squares would stay I would suggest to double the movement distance for all units. Going straight should cost 2 while going diagional should cost 3. Atleast then you would get fair movements.

 

[Nicol.Bolas]

the more sides the better.

since the debate is completely distant from the main point now: is it fun?

I suggest dodecagon grid for even more grid realism

http://en.wikipedia.org/wiki/File:Tile_46b.svg

its perfect..... the yellow and purple tiles would be tiles as well, so in reality it´s a combination of dodecagon, hexagon and square tiles

 

[Saarud]

the more sides the better.

since the debate is completely distant from the main point now: is it fun?

I suggest dodecagon grid for even more grid realism

http://en.wikipedia.org/wiki/File:Tile_46b.svg

its perfect..... the yellow and purple tiles would be tiles as well, so in reality it´s a combination of dodecagon, hexagon and square tiles

I can think of 2 ways I think it would be more fun... atleast for me.

1: No tiles at all. That is to say yes there has to be some sort of measure counting maybe in smaller pixels or so. Units have different sizes so they take up a number of pixels based on how big they are and that goes for cities and other objects that is placed on the map as well. That would be fun but I do see some problem with that.

2: Instead of rigid sized hexes or squares they make tiles that have different shapes like in Paradox ganmes. These tiles could of approx the same size as in Civ 4/Civ 5 but as they have different shapes they could border anything from just 1 to 20 other of these tiles.

 

[Farm Boy]

the more sides the better.

since the debate is completely distant from the main point now: is it fun?

I suggest dodecagon grid for even more grid realism

http://en.wikipedia.org/wiki/File:Tile_46b.svg

its perfect..... the yellow and purple tiles would be tiles as well, so in reality it´s a combination of dodecagon, hexagon and square tiles

I don't know about you, I am thoroughly enjoying the refresher and delve into game mechanics theory(thank god for gentlemen of math!) so yes, it is fun.

I am confused to how you think the debate is distant from the original post. This thread has been entirely on topic.