Civ III: Conquests Patch Notice

[Ridgelake]

Originally posted by T-hawk
If Charis' assumptions and calculations are correct, we'll need twice as many knights or cavs as we used to in these situations. This completely and totally changes the combat balance of the game.

Yes, it makes the Pyramids even godlier than they are now. If you can out-expand everyone else, and can stay in the neighborhood tech-wise, defending a far-flung empire will be much easier. Assuming you have resources (acquisition assisted by pyramids), you will be hard to dislodge.

There are so many implications of this proposed change, its mindboggling. The above one is just an example.

Irregardless, the bottom line here is that this proposed change will reduce the number of viable options available to reasonably accomplish a given task. These changes might make results more in-line with reality. But for a strategy game, reducing strategic options is not a good thing. That is the fundamental issue with this proposed change.

 

[Master Shake]

"R is now calculated as average of R_1, R_2, R_3, R_4, where each R_i is an independently-generated random "real" between 0 and 1"

I don't understand how this could drastically change the combat results.

Suppose I have a list of random values between 0 and 1. Now, suppose I group that list into fours, and replace each group with the average of its members.

I've now got two lists, one a quarter the size of the other.

But aren't the two lists "equally random"? (Sorry, I don't know the technical lingo here... Nor the technical concepts come to think of it )

What I mean is, if I'm using the first quarter of the larger list to aid me in some decision making, don't I have a good reason to think that over the long run, using the shorter (averaged) list will tend to produce the same results?

Can anyone help me out here?

-mS

 

[SirPleb]

Mike B, thanks for the correction about the combat calculation change.

But as others have said, the corrected description doesn't change the concerns being voiced in this thread - the result remains much the same.

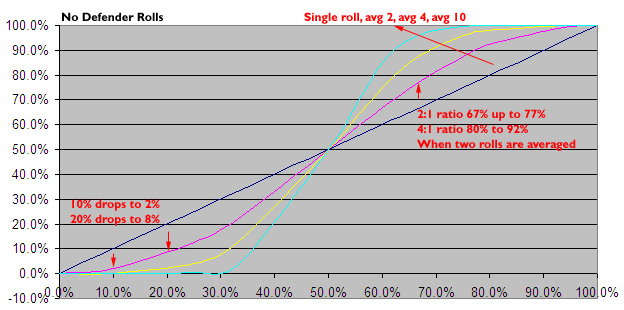
The change you describe does not affect streakiness except as a side-effect. What it does affect is the odds of a win when the attacker's strength (after all modifiers of course) is different from the defender's strength. The greater that difference, the more the odds change vs. the previous calculation method.

The sample cases posted by Arathorn for our latest understanding of this change show that the impact of the change is very large in some common situations involving contemporary units. (Not just the infamous spearman/tank.)

The strong will become stronger and the weak will become weaker. This greatly changes balance in the ways already pointed out in this thread (less strategic options, already strong unique units become overpowering, etc.)

I'm curious what the underlying motivation is for changing the combat calculation.

If the motivation is to reduce the odds of a spearman winning a single battle vs. a tank, then there are other ways to do that without affecting core game balance - why not use a technique which is specific to that class of problem without altering all other combat odds at the same time?

If the motivation is to reduce perceived "streakiness", why not do exactly that instead of altering the odds? That can be done by having combat calculations remember recent results and modify odds in each new battle to "correct" overall results toward the expected average. (The rate of convergence toward expected averages could easily be parameter controlled.) A change such as this would leave existing odds and combat calculators exactly as they are, but would reduce pure randomness by reducing the mathematically correct frequency of random streaks to better match the expectations held by most people And a change like this could be used in other areas such as leader frequency. You could maintain a proper average of 1 leader per 16 elite wins while hugely reducing the chance of long leaderless streaks (which are mathematically correct but feel wrong to most people, as well as making for frustrating gameplay.)

 

[padlock]

Originally posted by Arathorn
Padlock -- that's the same as my interpretation, except I divided everything by 1024 to get a float between 0 and 1. Except same concept but a slightly different way of phrasing it.

I agree that both our methods are equivalent. Also, having looked at your numbers further, I agree that if we are correct, then this is a major change which strongly limits a larger number of sllightly weaker units from defeating (and even substantially damaging) a smaller number of stronger units. In my opinion, this limits gameplay choices as is not a good thing.

 

[Grey Fox]

Originally posted by Arathorn
These are true but also mis-leading...spear should defend at 2.7, no?

Sorry, yeah I meant that.

 

[Master Shake]

The more I think about this the less I understand.

If the only change is that the random number is being replaced by the average of four random numbers, then it really seems to me as though overall, combat results would not change.

Someone here said the average of four random numbers between 0 and one tends to .5. Is that true? I can't figure out why it would be.

EDIT: Wait, now I'm starting to see. I guess I would be suprised if the average of a thousand random values was anything other than .5...

-mS

 

[eliliang]

Originally posted by SirPleb
If the motivation is to reduce perceived "streakiness", why not do exactly that instead of altering the odds? That can be done by having combat calculations remember recent results and modify odds in each new battle to "correct" overall results toward the expected average. (The rate of convergence toward expected averages could easily be parameter controlled.) A change such as this would leave existing odds and combat calculators exactly as they are, but would reduce pure randomness by reducing the mathematically correct frequency of random streaks to better match the expectations held by most people And a change like this could be used in other areas such as leader frequency. You could maintain a proper average of 1 leader per 16 elite wins while hugely reducing the chance of long leaderless streaks (which are mathematically correct but feel wrong to most people, as well as making for frustrating gameplay.)

In statistics, this method is called variance reduction. It is good for simulations, but I disagree that it would be good for a game, especially if it is multi-player with other humans. Variance reduction would allow a player to begin to "know the future"! I realize that this is the way that some gamblers gamble (wait! wait! red has come up 6 times in a roll! Time to bet on black!) but this doesn't make it right.

 

[LKendter]

I know why this is showing up - the people who can stand tank losses to spearman.

I have been involved in 58 sg, over a dozen gotm, and plenty of solo games I am not taking this one lightly. I helped a win in a 5-city conquest game at deity and several other crazy deity variants. I have no question I will beat Sid at some point.

Tanks versus mechs will get even harder. That ruins the 5cc challenge. A knight versus muskets behind walls or size7 gets harder. A Cavalry vs. Musket man is already nasty for the cavalry side. Do we really want the era even more favoring the attacking?

Cavalry vs. Infantry is doable with artillery. An attack of 6 vs. defense of 10 works when it is 4 hp vs. 1 hp. With the new combat the game will stalemate from the arrival of Infantry until Tanks appear.

If this option must be added - make it an option in preferences! The games combat works well with the hp system in place. Don't fix the gpt / fp issues and destroy combat.

 

[eliliang]

Originally posted by Master Shake
The more I think about this the less I understand.

If the only change is that the random number is being replaced by the average of four random numbers, then it really seems to me as though overall, combat results would not change.

Someone here said the average of four random numbers between 0 and one tends to .5. Is that true? I can't figure out why it would be.

EDIT: Wait, now I'm starting to see. I guess I would be suprised if the average of a thousand random values was anything other than .5...

-mS

Exactly (on your edit).... From my message to Mike:

Think of the attacker rolling a 10 sided dice with sides numbered from 1 to 10. Say that the defender has a defense value of 4. So as in your example, if the number rolled is greater than or equal to 4, the attacker hits, otherwise the defender hits. In this scenario, with one roll, the attacker hits 7 out of 10 times or 7/10 probability of the attacker hitting. Your example might be that we roll the dice 4 times and take the average. Well lets take this to an extreme so that I can graphically show you the effect of this change in distribution. Let's say that we roll the dice a TRILLION times and take the average of these rolls. What is the result? Intuitively, you should sense that the average will tend to stay close to the mean, or 5 1/2. Well 5 1/2 is greater than 4. Even without computing the exact odds, I think you would agree that in this case, the odds that the average are greater than or equal to 4 is much greater than 7/10 now.

 

[Master Shake]

I think the best idea would be just to give higher teched units more hitpoints.

If a spearman has three hitpoints, a tank should have like 15 or something. After all, one good punch to the face and a spearman is down, while if you do the same to a tank you just break your knuckles.

But in any case I don't think I'm bothered with the patch as is. If it were up to me, a spearman would *never* beat a tank. That's just silly.

-mS

 

[Charis]

Ok, let's try things without the defender roll, as suggested by Alexman and Arathorn.

The key thing is this is back to a symmetric graph. (The asymmetry came from using two rolls but averaging only the attackers). This new graph is shown here -- as in Arathorn's post it compares a random (0,1) die roll vs the A/(A+D) value. The straight line is one roll as now, and the other lines show averaging two, four or ten rolls...

As with the other examples I gave, these are still the chances to win a single hp shot. Since each fight faces multiple hit points, the actual results will be steeper than shown here. A 67% initial chance to win (2:1 like MDI vs a plain spear) would get converted by this avg-of-two process to an 83% chance for a given hp, which for vet-vs-vet combat means a 98% chance for the unit to win. (Yowza!) Let's look at T-Hawk's main concern, something like knight vs city-fortified muskets, 4 on 7 (similar to cav on rifle of 6 to 10.5). Current system, chance to win 1hp is 36.4%, and chance to win vet on vet is 22%. With the avg-two approach that Mike B suggests, 36.4% will drop down to 25% for each hp, or for the whole battle, 7.1% chance to win. He's right on target with his fear, the chance to win is three times less. Accounting for retreats and using extra fresh units to hit ones you hurt, this does mean you'll need to produce literally twice as many knights to take the same city. That's significant, and that's one of the semi-close situations, not one of the higher odds situations. I tend to agree with the comments of SirPleb, Ridgelake and LKendter in addition to the others cited.

Charis

 

[Louis XXIV]

I honestly don't think there will be this much affect.

Take this battle calculator here

http://www.zachriel.com/BattleCivulation.asp

Try setting the amount of times you want to simulate the attack down to ten. You'll notice it can produce some wild difference (like 80% chance to win for the Swordsman). If you set the number of trials to 40, you get numbers closer to what you'd expect. If you set the number to 1000, its even closer. I think that's really what is being affected here (since it averages some rolls that are higher than expected and lower than expected down to right where it is expected).

What it would end up doing is Tank vs Spear (a little more than an 88% chance) and reduce the amount of times you get a fluke roll, and the Spearman gets the win

 

[Arathorn]

Master Shake. The difference is that averages are always much closer to the middle than truly random numbers. Your expected deviation between numbers goes down greatly.

Asking a program I have for 12 random numbers between 0 and 1023, I get: 205, 202, 694, 914, 133, 779, 145, 802, 432, 321, 1001, 798. Averaging four at a time I get 504, 480, 638. Notice how the first list has a lot of more extreme numbers (3 under 210 and 2 over 900) while the second list is clustered around 512. This would happen even I had a list of 12 "averaged" numbers -- the "averaged" numbers will cluster much closer to the middle of the interval while the random numbers are equally distributed across the entire interval.

@SirPleb: I'm curious how you would implement a "self-correcting" PRNG or whatever you're describing without making it too exploitable (Oh, I lost three in a row at even odds in this unimportant battle. Time for the important one until I get good luck for a bit and then back to the one that doesn't matter). Is there an article I could read or something? You mention parameters, so it seems you have something in mind, but I'm not aware of any such system (not that my knowledge in those particular things goes particularly deep).

Arathorn

 

[Arathorn]

Charis, I get more like 26% for the knight to take a hp from the musket -- but that's assuming two rolls. Mike said there would be *4* rolls, so that's down to 18% (about 18.32% in my couple hundred thousand trials) for each hp. That's a 2.45% chance for the knight to win, assuming no retreats. It was 22.29% before. Twice as many? Probably more like 3-4 times as many as before. With contemporary units....

@Louis -- it's not re-rolling the entire combat -- it's rerolling each hp of the combat. Very different.

Arathorn

 

[eliliang]

Originally posted by Arathorn
@SirPleb: I'm curious how you would implement a "self-correcting" PRNG or whatever you're describing without making it too exploitable (Oh, I lost three in a row at even odds in this unimportant battle. Time for the important one until I get good luck for a bit and then back to the one that doesn't matter). Is there an article I could read or something? You mention parameters, so it seems you have something in mind, but I'm not aware of any such system (not that my knowledge in those particular things goes particularly deep).

Arathorn

This is what I was referring to as being able to know the future.

Here is a nice page on variance reduction: explanation of variance reduction

 

[eliliang]

Originally posted by Louis XXIV
I honestly don't think there will be this much affect.

Take this battle calculator here

http://www.zachriel.com/BattleCivulation.asp

Try setting the amount of times you want to simulate the attack down to ten. You'll notice it can produce some wild difference (like 80% chance to win for the Swordsman). If you set the number of trials to 40, you get numbers closer to what you'd expect. If you set the number to 1000, its even closer. I think that's really what is being affected here (since it averages some rolls that are higher than expected and lower than expected down to right where it is expected).

What it would end up doing is Tank vs Spear (a little more than an 88% chance) and reduce the amount of times you get a fluke roll, and the Spearman gets the win

Yes, and if you run it enough times, then the tank always wins. So how does this not affect the probability of a tank vs. spearman win?

 

[dannyevilcat]

I think all of this concern over a revised combat system is funny, considering how badly it was recieved in the first place.

 

[Louis XXIV]

Originally posted by eliliang


Yes, and if you run it enough times, then the tank always wins. So how does this not affect the probability of a tank vs. spearman win?

I'm not concerned about the Tank vs. the Spearman, I'm a lot more concerned about a Longbowman vs. a Spearman. Also, its not being run infinate times, just 4.

If people say that it makes a Longbowman have a significant chance to win, than I'd be concerned. If it change slightly, so units that should win almost all the time loose even less (Spears shouldn't loose all the time, a lot closer to 2/3 the time), I don't mind it.

 

[eliliang]

Originally posted by Louis XXIV


I'm not concerned about the Tank vs. the Spearman, I'm a lot more concerned about a Longbowman vs. a Spearman. Also, its not being run infinate times, just 4.

If people say that it makes a Longbowman have a significant chance to win, than I'd be concerned. If it change slightly, so units that should win almost all the time loose even less (Spears shouldn't loose all the time, a lot closer to 2/3 the time), I don't mind it.

It does significantly increases the probability of a longbowman win over a spearman, but spearmen still don't always lose.

 

[SirPleb]

Originally posted by Arathorn
@SirPleb: I'm curious how you would implement a "self-correcting" PRNG or whatever you're describing without making it too exploitable (Oh, I lost three in a row at even odds in this unimportant battle. Time for the important one until I get good luck for a bit and then back to the one that doesn't matter). Is there an article I could read or something? You mention parameters, so it seems you have something in mind, but I'm not aware of any such system (not that my knowledge in those particular things goes particularly deep).

I'm not sure how I'd implement it, I was making it up as I went along I have little knowledge of these things. I suspect that eliliang could point us to an article. [Edit: cross-posted, I see that he already has done so, thanks eliliang!]

I think you and eliliang are right, there may not be a way to do it without introducing something that advanced players could exploit by knowing the future. Perhaps that is affected by how rapid a convergence is used. If the objective is only to make very long streaks much less likely, a small convergence could be used, and that could be very difficult for a human to take advantage of. Even after losing a battle which was likely to be won, we wouldn't know that odds are better than average for the next battle unless we take into account the previous N (perhaps 4 or 5?) fights. Perhaps this kind of algorithm would have to be tried to see whether it could have a useful impact without also creating an abusable loophole. Or perhaps there's already literature analyzing this kind of thing.

At any rate, my question to Mike B remains, if the intent of this combat change is to reduce streakiness, why not shoot for a technique which addresses it without affecting other things? (If there's no such technique, then that's that, the problem can't be solved without side-effects. And perhaps should not be solved - with side-effects such as we see in the described change, the cure seems definitely worse than the disease.)

Off the topic of combat, I do think I'd like to see variance reduction applied to leader generation. I don't think that knowledge of slowly and slightly increasing leader odds would result in abuse; if anything it would increase strategic options by permitting the assumption that a certain number of wins will sooner or later include a leader in the results.