Science & Technology Quiz 2: The one with the catchy title.

[GoodGame]

Is the surface area of contact of both hits, equal? Is the same amount of energy used to generate each hit?

 

[SS-18 ICBM]

Yes .

 

[Perfection]

punch that stops at the target

 

[GoodGame]

Is the surface area of contact of both hits, equal? Is the same amount of energy used to generate each hit?

Yes .

Then they both hit with the same force. I assume the jab pulls the punch after contact, but assuming it holds it long enough for the momentum to be transfered, then they both hit the same. If not then the punch that stops transfers more momentum and therefore "hits harder".

 

[SS-18 ICBM]

Just realized my question was stupid. Open floor.

 

[Veritass]

I remember an experiment in high-school physics where we measured the kinetic energy transfer of a pliable mass (think Silly Putty) that was thrown at an object, versus the same mass at the same velocity that bounces off the object. The object that bounces off delivers about twice the kinetic energy of the object that sticks, because its velocity goes from x to -x, and the one that sticks goes from x to 0. So you need to throw your punch and make sure it bounces off.

========================================================

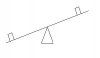
Anyway, here is my problem: you have a balance with a fulcrum in the middle, and it is balanced and level. You place a 10-gram weight on the left side, and the left side goes down. You place a 10-gram weight on the right side equidistant from the fulcrum, and the balance returns to level.

At the point in time when you have just set the second weight on the right side, what is the force that overrides the inertia and causes the right side to go down?

Spoiler :

Don't just say "gravity", because at that point in time the gravitational pull should be the same on each side.

 

[theskald]

The effort! The load! The leverage! Other nouns related to levers!

 

[GoodGame]

Technically, isn't the fulcrum kind of like a shaft that the board rotates around (though incompletely of course)? So then wouldn't the force making the right side descend be rotational force, a.k.a. 'torque', with gravity being the source of the force, of course.

 

[Veritass]

Technically, isn't the fulcrum kind of like a shaft that the board rotates around (though incompletely of course)? So then wouldn't the force making the right side descend be rotational force, a.k.a. 'torque', with gravity being the source of the force, of course.

There is no torque involved. In the simple picture presented, there is no torque to be had: there is only gravity pushing equally on the left and right sides.

 

[Perfection]

I'm going to guess the normal force that kept the beam from falling to the ground.

I would like to see a formal account of this / references.

 

[Veritass]

I'm going to guess the normal force that kept the beam from falling to the ground.

I would like to see a formal account of this / references.

I'm afraid that I don't understand what "normal force" you are referring to. The system was at equilibrium with the weight only on the left side, and the left side pushed down and resting, say, on the table. The system "should" have still been at equilibrium after the addition of the weight on the right, but what force would cause it to return to level?

 

[Perfection]

Normal forces are simply contact forces exerted by stuff. The force your desk exerts on your computer to hold it up is a normal force.

I'm saying the force of the table pushing up on the left side.

I don't buy it, but it's the only other force I can see in the system (other then the force of the fulcrum, which can't produce any torque). Frankly, I'm skeptical that the arm would return to a balanced position.

 

[Simple Simon]

force1*moment arm(force1) = force2*moment arm(force2) for equilibrium


Gravity is responsible for pulling both sides down. Since we assume the beam to be inflexible, the side on which force*moment arm(force) is bigger will create the larger torque in the bearing, and sink. When you place the second weight down, and create perfect equilibrium, then nothing happens!
.

So either you must jiggle the assembly slightly (which will usually happen when you place a weight down), or you must create a larger force*moment arm(force).

Frankly, I'm skeptical that the arm would return to a balanced position.

indeed - why would it?

 

[GoodGame]

indeed - why would it?

Why wouldn't it? It's a perfectly symmetrical center-balance, with equal weights on both sides. The only real-world issue blocking going to equillibrium is that the balance board is in contact with the ground, so there might be some friction there, and assuming the weights don't slide on the balance board either, due to gravity.

 

[Veritass]

When you place the second weight down, and create perfect equilibrium, then nothing happens!.

This is correct so far. In the first example drawing, placing the equal weight equidistant from the pivot point would not cause the beam to return to level. Then how does a balance work and go back to level? See second drawing attached.

 

[uppi]

This is correct so far. In the first example drawing, placing the equal weight equidistant from the pivot point would not cause the beam to return to level.

Actually, for real systems the balance wouldn't be on a point, but on a surface with a width larger than zero. A real balance made like this, will return to level, because pushing one side down will move the pivot point in that direction and give the other side more leverage. Try balancing a ruler on your finger and it will oscillate around the level position.

Then how does a balance work and go back to level? See second drawing attached.

A balance has something that in the level position points down from the rotation axis (I don't know how to call this...). If the scale is tipped in one direction, this will move in the other direction and will create leverage to balance it, as long as the force difference is within limits.

 

[Veritass]

Uppi has both solutions and is declared the winner. Both solutions involve moving the point of balance horizontally when the scales move vertically.

Option #1: The rounded fulcrum (e.g. the finger with the ruler balanced on it) causes the point of contact to move. When the weight on the left side goes down, the point of contact moves to the left. Then when the equivalent weight is added to the right side, it is farther from the point of contact, so its weight is leveraged more.

Option #2: A typical scales (see the attached figure) has its balance beam set off from the point of rotation. The small almost-vertical bar attached to the lever has the point of rotation at the top of this bar. Thus, when the right scale is pushed down, the entire beam is shifted slightly to the left. This brings the right scale closer to the rotation

point, and the left scale further from the rotation

point. When the equivalent weight is added to the left scale, it is farther from the rotation

point, so its weight is leveraged more.

Take it away, Uppi!​

 

[uppi]

What's a density matrix and what information can be obtained from one?

 

[Simple Simon]

What's a density matrix and what information can be obtained from one?

I use a density matrix to assign a non-uniform density to physical objects in CAE modeling - but I am very sure that this is not what you want

It has to do with quantum systems, methinks

 

[uppi]

I use a density matrix to assign a non-uniform density to physical objects in CAE modeling - but I am very sure that this is not what you want

I admit I don't know anything about that, but wouldn't you need a 3D structure instead of a matrix for that?

It has to do with quantum systems, methinks

Yes, that's the right track.