A general question. I recently saw some of the more impressive fractal ones (particularly the following, which is likely the most impressive progression i have seen  ) :
) :

It is one of the so-called 'strange-attractors', and you can easily find articles on that online.
As for the more usual geometrical shapes:
-The Regular Tetrahedron
It is the smallest (and sharper-edged) of the five regular polyhedra. Consisting of four trianges of equal form.

In the Socratic dialogue about Science, Plato presented the claim that if all fundamental materials in the cosmos consist of regular polyhedra, then the tetrahedron would be the undivisable part of Fire (due to the very sharp edges, which would supposedly harm instantly, like fire does).
-The Hyperbola (presented in a Conic system)

It is of interest that it is the only conic section which gets presented not in a single cone, but a system of two cones, one of which is inverted (and systems with two cones in this formation are also used for various symmetrical examinations, as in Physics and Einstein's work). Given this name by Apollonios of Perge, in the early Hellenistic era, in his work "Conics".
-Spiral of Theodoros of Cyrene
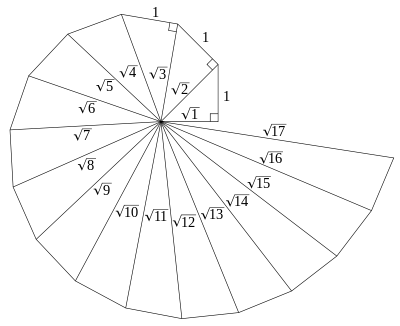
Again discussed in Plato's work, this spiral was studied in the 5th century BC and onwards, and was about providing proof of the irrationality of a number of square roots of integers. It should be noted that the spiral's turns soon lead to an approximation of Pi, for one of its main properties. Also there is no intersection of the lines (apart from the obvious one in the core) nomatter how much the spiral expands.
*
You can post your own favorites, and maybe discuss them if you wish.
 ) :
) :
It is one of the so-called 'strange-attractors', and you can easily find articles on that online.
As for the more usual geometrical shapes:
-The Regular Tetrahedron
It is the smallest (and sharper-edged) of the five regular polyhedra. Consisting of four trianges of equal form.

In the Socratic dialogue about Science, Plato presented the claim that if all fundamental materials in the cosmos consist of regular polyhedra, then the tetrahedron would be the undivisable part of Fire (due to the very sharp edges, which would supposedly harm instantly, like fire does).
-The Hyperbola (presented in a Conic system)

It is of interest that it is the only conic section which gets presented not in a single cone, but a system of two cones, one of which is inverted (and systems with two cones in this formation are also used for various symmetrical examinations, as in Physics and Einstein's work). Given this name by Apollonios of Perge, in the early Hellenistic era, in his work "Conics".
-Spiral of Theodoros of Cyrene

Again discussed in Plato's work, this spiral was studied in the 5th century BC and onwards, and was about providing proof of the irrationality of a number of square roots of integers. It should be noted that the spiral's turns soon lead to an approximation of Pi, for one of its main properties. Also there is no intersection of the lines (apart from the obvious one in the core) nomatter how much the spiral expands.
*
You can post your own favorites, and maybe discuss them if you wish.





