(+) Influence
taiwans elite businessman
- Joined
- Jul 30, 2004
- Messages
- 170
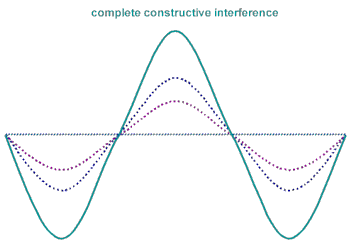
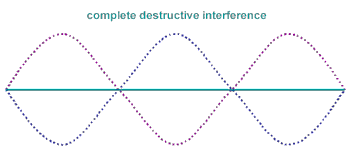
I'm no scientist so pardon my ignorance on this topic. Is it true that when two signals of the same frequency meet, it's possible for them to have "destructive interference" and become 0? If that's the case, would I be able to put two speakers together (in calculated distances apart) so that they each produce a sound, but together the sound cancels?