Since I have [snip]-all to do all day at work, I thought I'd spend some time explaining the mechanics of this thing, in an attempt to make this understandable for non-mathematicians/statisticians as well. But don't worry, if you don't understand it, either my didactic skills are insufficient or the matter is just too complex.
Anyway, so here goes...
The scores entered here are actual or
observed scores.
But based on players and civilizations their previous scores made, one can make an estimation of what score a player would get playing another civilization. If player John's score is 225 and Egypt's score is 144, one could estimate that if John would play as Egypt, his score would be √(225*144)=180. (This is the
geometric mean, rather than the
arithmetic mean.)
180 would be John's
expected score.
Now, what I do is calculating the scores of all players and civilizations thus, that all expected scores are as close to the observed scores as possible. As long as there are no
conflicting scores (my coined term, which I will explain later), the expected scores can actually be equal to the observed scores.
Please take a look at the first picture. This shows all the submitted results. Each line is one game: that player played with that civilization. As you can see players who played as the Zulus never played with any other civilization. Therefore that group is incomparable with the rest. But we've reached a funny situation, where almost all results are linked in some manner, but there are very few conflicting results. It's all loose ends, except for zbgayumn & gram123 / Egypt & Inca. That's the only place where you can go round and the only place where there are conflicting results. The scores for those two players/civilization cannot be fit as such that the expected scores are equal to the observed scores.
Ironically, conflicting results is what we want! The more conflicting results, the more statistical cases we have, the lower the margin of error.
You can see how this works out in the table / picture two. Note that these scores are squared. (e.g. √40000=200) To the right and bottom of the right table you see scores below or above 1, corresponding to the player/civ at the left/top. In the bottom right corner you see 312, which is the global average. The expected score of evil_spock playing as the Inca is 2.1*0.6*312=383. In red you can see the conflicting scores. Zbgayumn actually played better with Egypt and worse with Inca than expected.
Gram123 actually played worse with Egypt and better with Inca than expected.
In short, the present scores make little sense...yet! The longer this thing continues, the more accurate and fair the score list will be. What we need is more red number/black lines. And of course all scores linked together. At the moment there are only three civilizations not linked to the main blob yet.
For fun I made another chart (last picture) which has no functional meaning, but just illustrates the dynamics of new scores coming in. Each line is a group of results that is not linked to other results. Eventually they will all merge into one. The thickness of the line represents the total number of results within that group, the height the average score of that group.
Impressive result you got there! I think this is very interesting too. Makes you wonder whether it's better to squeeze out a victory on the highest difficulty level you can handle, or to totally dominate a game on an easy difficulty?
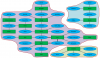
Apparently. Ok, I'll upload it tonight again. I don't know how or why I removed it, though. 
