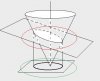
Hm, but if both focus points of an ellipse are on the conic axis, then they have to be both the very same point, not different points on the axis. If they are both the same point there there is only one focus in the ellipse, which by definition means it is not an ellipse but a circle.
A circle *is* an ellipse, in the same way that a square *is* a rctangle.
By contrast, an ellipse pressuposes that there are two cones formed by the uneven section of the actual cone (as shown, again, in fugure 2) which is why it has two focus points (if it was a circle, then the two cones would be entirely symmetrical to each other in regards to their common base, which is not so in those which form an ellipse).
I'm not following this. Where did you get those first two pics from? You construct/define an ellipse by intersecting a cone with a plane, rather than trying to construct two different cones around an ellipse (sort of, anyway). It's hard for me to tell if those cones are meant to have a circular base or not, and it looks to me like the point of the cone isn't in the centre of the cylinder the picture also shows. *edit* If you put the axis of that cone you draw to be parallel to the cylinder, then it won't be in the centre of the cylinder./you won't have a circular cone. If you connect the focus to the centre of the cylinder's base, and call that your axis, then you also won't have a circular cone, and the axis won't be parallel to the cylinder. I think you've just read too much into a non-accurate diagram, but I'm not sure without seeing more labels/what the diagram is trying to show.*/edit*
If you do try and reconstruct a circular cone above & below an ellipse like that, the two cones should be the same, just rotated 180 degrees, and the foci shouldn't be on the cones' axis (unless it's a circle).
Furthermore the fact that only one of those points is termed as "real" seems to signify it has some special characteristic in regards to the other one, which is termed as "empty". So if that special characteristic is not that it is part of the axis of the original cone, what is it?
Just something someone made up. It's not a 'real' focus, it's a 'full' focus. More to the point, it's a focus that is inside the sun, because of the huge difference in relative mass. Look at
http://en.wikipedia.org/wiki/Gravitational_two-body_problem with two bodies of similar mass, both move in ellipses, and both have 2 'empty' foci. And if you made a model of just earth & sun, the sun would also move in an ellipse, it'd just be a very small ellipse, if you made a track of the centre of mass, it'd never be outside the rest of the sun, and you could say both foci are 'full'.
(ps i will now go read about the dandelin spheres, but would like a reply to this post too if possible

)
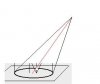
Edit: I now looked at the Dandelin spheres, here is an image of them:
I noticed, though, that in this image the conic section is in an inverted angle to the cone than the one in the images i posted before.
This has to play a very significant role in regards to the system as a whole, so again i ask if in the other case of positioning of the section in regards to its angle to the base/pinnacle of the cone it remains true to say that one of the focus points will always be on the conic axis

Neither of the focus points will be on the conic axis, unless the ellipse is a circle, in which case both will be. (but again, I haven't actually sat & proved it, I've only done enough to convince myself.)
If you want to visualise why, imagine you have that top sphere in the end of your cone. Now, turn the cone upside down. The very top of the sphere will be on the conic axis, yeah? Rest your plane inside. If it sits perfectly on top of the sphere, you'll get a circle. As you start to angle the plane in any direction, the one point where it touches the sphere will move, the further you tilt it, the further down the sphere the contact point moves, and the less circular the ellipse you get from where the plane & cone meet. Does that make sense? Now, that single point where the plane touches the circle (F1 in the diagram) is actually the focus of the ellipse made by that plane. (and if you then drop a much bigger sphere in, so it rests on top of the plane, the point where that one touches (F2 in the diagram) is the other focus) So the focus won't be on the conic axis.
As for the bit I bolded, yes it does. It's called the eccentricity of a conic section. You can basically think of it as the angle of the plane divided by the angle of the side of the cone. If the eccentricity is zero (meaning the plane is perfectly horizontal in your diagram) it makes a circle. If the eccentricity is less than 1, you get an ellipse. If the eccentricity is exactly 1 (meaning the plane is parallel to the side of the cone) you get a parabola. If the eccentricity is greater than 1, the plane will cut both the top & bottom sections of a double cone, and give you a hyperbola.









 )
)