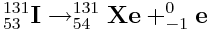Let's discuss Mathematics

[ParadigmShifter]

Calculating permutations of objects I believe.

EDIT: Nope, I was thinking of factoradics. http://en.wikipedia.org/wiki/Factoradic

Factorions are just a numerical curiosity it seems.

http://en.wikipedia.org/wiki/Factorion

 

[SS-18 ICBM]

I suspected as much. Thanks for the answer.

 

[emzie]

How is Pi calculated so precisely (the super computers taking it to billions of decimal places)?

 

[Atticus]

http://forums.civfanatics.com/showthread.php?p=5197851#post5197851

Also, computers probably use the knowledge that
sin x = x + (x^3)/3! + (x^5)/5! + (x^7)/7! +...

 

[Mise]

http://en.wikipedia.org/wiki/Approximations_of_π

A very interesting read!

 

[dutchfire]

From that article:

These approximations have so many digits that they are no longer of any practical use

What wiki said!

 

[nc-1701]

Any suggestions on a good cryptography/cryptanalysis book? I don't have experience with either, but I do have a decent (undergraduate) background in Abstract Algebra and Number Theory. So I want something introductory, but very technical and applicable to preparing to go deeper into the subject (possibly in grad school).

 

[IdiotsOpposite]

From that article:


What wiki said!

But it's true! Any more than 50 digits is useless on a practical, physical scale!

 

[IdiotsOpposite]

Well, I'm bored, so here's a small challenge. Prove that the following union of sets, where a and b are positive integers:

contains b* distinct elements if and only if a and b are coprime.

Probably easily done, but hey.

*: or is it b-1 distinct elements...

 

[Atticus]

What the frac? Is it a typo?

 

[IdiotsOpposite]

frac denotes the "fractional part" of a function. It can be defined as frac(x) = x - floor(x).

 

[Atticus]

Ok, I thought you had mistyped /frac in LaTex.

Gonna think this later. Maybe tomorrow when it's Friday.

(Oh, and then x doesn't denote Cartesian product perhaps?)

 

[IdiotsOpposite]

Ok, I thought you had mistyped /frac in LaTex.

Gonna think this later. Maybe tomorrow when it's Friday.

(Oh, and then x doesn't denote Cartesian product perhaps?)

Nah, just a times. I didn't want it to look like a "bfrac" function, cause that wouldn't make sense.

 

[Petek]

I'll post my solution in a spoiler in case others want to solve the problem. I propose that we use {x} to denote the fractional part of x, to make the notation easier. So, we want to show that if a and b are positive integers, then the expression

b{na/b}

assumes distinct values for n = 1, 2, ..., b iff a and b are coprime.

Spoiler :

First, suppose that a and b are coprime. By the division algorithm, there exist integers q_n and r_n for n = 1, 2, ..., b such that

na = q_nb + r_n

with 0 < r_n < b if n = 1, 2, ..., b-1 and r_b = 0. (That only r_b = 0 follows from a and b being coprime.)

Now, b{na/b} = b{(q_nb + r_n)/b} = b{q_n + (r_n/b)}

= b{r_n/b}
= r_n

because r_n < b for all n. Therefore, it suffices to prove that the r_n are distinct.

Suppose that r_n = r_m but n =/= m. The equations

na = q_nb + r_n
ma = q_mb + r_m

imply that

(n - m)a = (q_n - q_m)b

which implies that b divides the product (n -m)a. But since a and b are coprime, we see that b divides (n - m). Since 1 <= n, m <= b, we must have that n = m, contradicting the assumption that n and m are unequal. Therefore, the values b{na/b} are distinct.

Conversely, assume that a and b are not coprime. Let d = gcd(a,b) > 1. Then there exist integers a₁ and b₁ such that

a = a₁d
b = b₁d

with a₁ and b₁ coprime. We show that b{na/b} = b{ma/b} for n = 1 and m = b₁ + 1. Thus

b{(b₁ + 1)a/b}
=b{a₁ + (a/b)} (some algebra omitted here)
= b{a/b}

so the values of b{na/b} are not distinct, as required.

 

[azzaman333]

So, I'm trying to prove something which has summations in it for one of my uni assignments.

Am I allowed to, for example, take something like sum,i=1,n[xi(yi-xi) - z (yi - xi)] and split that into sum,i=1,n(xi-z) * sum,i=1,n(yi - xi) ?

I hope that makes sense.

 

[Atticus]

So you're summing up terms
x_i(y_i-x_i) -z(y_i-x_i)
=(x_i-z)(y_i-x_i),
right?

And you are hoping that the sum of these products is the same as the product of sums? That's not the case. Simple example:
2*5 +3*4 +1*1 is not (2+3+1)(5+4+1).

 

[azzaman333]

I had a feeling my logic was flawed... stupid proofs...

 

[Atticus]

What are you trying to prove?

 

[azzaman333]

SST = SSR + SSE. I was trying to understand how what I had in my notes worked, and whether I could replicate it, but seems I couldn't.

 

[Earthling]

So you're summing up terms
x_i(y_i-x_i) -z(y_i-x_i)
=(x_i-z)(y_i-x_i),
right?

And you are hoping that the sum of these products is the same as the product of sums? That's not the case. Simple example:
2*5 +3*4 +1*1 is not (2+3+1)(5+4+1).

I'm not sure what helps azzaman with his original problem because his wording and context is a little confusing, but your example doesn't match what he wrote. In fact, what he wrote is certainly true in simple instances, really just distributive property, for example:

3*(5-3) - 2*(5-3) = (3-2)(5-3) = 2

If you're dealing with finite numbers in your sequence I don't see what's wrong with what azzaman said first, maybe if the x_i and y_i values diverge you might not be able to do that, I didn't really look into it further.

edit - ok, I was so caught up in responding to Atticus that I missed what should be part of an the answer to azzaman's question.

You can't actually split up the summation just like that. You can just rewrite it as (xi-z)(yi-xi) though inside the sum, if that helps.

In fact I might have miscontrued Atticus post in that it seemed like he was attempting to give a counterexample to the first part of his post in the second when maybe he wasn't. The example he gives matches the problem with what azzaman was attempting.


final edit for azzaman -I don't know what you are actually trying to prove and whether it's much simpler, but if you need an anvil to hammer a nail just using the Cauchy-Schwarz inequality could help you azzaman, or what you need for your proof might be found in a component of that proof.