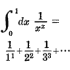Why is mathematics boring/difficult to/for many people?

[Perfection]

Because it proves that the axiom of choice gives rise to a physically impossible result. (then again the non-measurable subsets are a problem too. They assume a continuum theory of matter, which is impossible at the atomic level)

Yeah, but that doesn't seem that interesting to me, that's true of all mathematics. Adding a pile of dirt to a pile of dirt makes a big pile of dirt not two piles of dirt.

 

[Truronian]

It was a reflex action; you're just being obtuse.

(Why do these maths threads always end up as pun wars?)

cos mathematicians are naturally funnier.

 

[StarWorms]

Yeah, but that doesn't seem that interesting to me, that's true of all mathematics. Adding a pile of dirt to a pile of dirt makes a big pile of dirt not two piles of dirt.

Well technically it would make one pile of dirt that is twice as big

 

[frob2900]

Yeah, but that doesn't seem that interesting to me, that's true of all mathematics. Adding a pile of dirt to a pile of dirt makes a big pile of dirt not two piles of dirt.

The spirit of invention and curiousity at work right here!

 

[Chandrasekhar]

The reason I prefer Maths over English, History etc. (although I do like History) is because I don't have to write any essays. Any amount of boredom is worth that, IMO.

Yes! Absolutely true. I've never found math to be dificult or boring, but even if it was... It would be much preferrable to essay writing.

 

[Perfection]

Well technically it would make one pile of dirt that is twice as big

Tehnically you're assuming the two drit piles are the same size

 

[Godwynn]

I've often heard people say "Ooh, math's is not my thing" or "Ooh, my brain can't handle that" about mathematics, whereas the same people would often choose other statement if some other difficult subject such as biology or the playing the piano came up.

I have reached the conclusion that the correct translation of the above statements might be "I find the subject boring and I do not wish to spend any time on it". Is that a correct translation?

If so, why is it boring to many people? Certainly other abstract subjects like aesthetics or art are not considered so, so why math?

If not, why is mathematics so difficult? From experience I know that the discipline needed to learn math is certainly no larger than that needed to learn to draw well, or, I guess, learn woodworking?

Why is a subject which is arguably as important as spelling considered a pariah in our modern world?

At first I had a hard time with calculus, after studying for a while I grew to like it and whizzed through it.

Next up is statistics.

 

[frob2900]

At first I had a hard time with calculus, after studying for a while I grew to like it and whizzed through it.

Next up is statistics.

If you can do calculus statistics should be easy (at least the statistical distribution parts, which is where a lot of emphasis is put in more advanced statistics courses)

 

[Integral]

At first I had a hard time with calculus, after studying for a while I grew to like it and whizzed through it.

Yes! Another one has seen the light! This made my day.

Integral

 

[Godwynn]

Yes! Another one has seen the light! This made my day.

Integral

At first I did try to use brute force memorization to learn it. Once we started getting into its application I really loved it. Calculus will be very helpful to me in the future after I get my Finance and Business Economics degrees.

BTW, interesting mathematics forum.

 

[warpus]

Because most people have short attention spans and/or are stupid.

 

[ParadigmShifter]

The Banach-Tarski paradox isn't comparable to piles of dirt though. It says you can cut up a ball into a finite number of pieces (24, if I recall correctly) and put them back together again to make 2 balls that don't just look the same, but are in fact exactly the same. So it's like taking a pile of dirt and moving it around and getting 2 piles of dirt that are exact copies of the original pile of dirt.

Of course, as frob pointed out, it does assue that matter is continuous (i.e. not made of atoms) and the cuts you have to make are fractal in shape so you can't use a knife to make the cuts.

 

[nihilistic]

Because it proves that the axiom of choice gives rise to a physically impossible result. (then again the non-measurable subsets are a problem too. They assume a continuum theory of matter, which is impossible at the atomic level)

No, it demonstrates the extent to which bijective functions do not preserve volume. Basically, this theorem says that bijective functions will not preserve volume even if you make it piecewise orthogonal with a finite number of pieces.

 

[Gogf]

My theory is that people don't bother to learn why they're supposed to do certain things. I would imagine that trying to solve problems with the minimal amount of thought possible makes math harder and less interesting.

 

[GenMarshall]

Mentaly, I cant process manipulating numbers in my head.

I can manipulate words, Japanese Kanjis, Katakanas, and Hiraganas. But I am compleately Dyslectic when it comes to processing numbers in my head.

 

[raen]

People think its boring and all Because you have to follow it along the years, if you loose the train in the way it gets harder, and people are not interested in what they dont understand.

I like deterministic maths and hate Probabilities (non-deterministic).

 

[Perfection]

No, it demonstrates the extent to which bijective functions do not preserve volume. Basically, this theorem says that bijective functions will not preserve volume even if you make it piecewise orthogonal with a finite number of pieces.

Okay, now that's interesting!

 

[frob2900]

Yes! Another one who has seen the light! This made my day.

Integral

Your avatar would be cooler with an actual integral, rather than just the definition. Here's an integral I always though was cool:

 

[TheBladeRoden]

Math is for computers, and people who are better at math than I am.

 

[raen]

Your avatar would be cooler with an actual integral, rather than just the definition. Here's an integral I always though was cool:

Integral and primitive are cool things, I like it very much