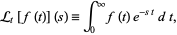ParadigmShifter
Random Nonsense Generator
Oh yeah 
Let's discuss Mathematics
- Thread starter ParadigmShifter
- Start date
Speaking of set theory, I saw Axiomatic Set Theory and the Continuum Hypothesis by Smullyan in bookstore, relatively cheap, and thought of buying it.
It's Von Neumann–Bernays–Gödel set theory though, which I've heard is a lot nicer than ZFC, but I hear it rarely mentioned. People are always talking about ZFC, so I suppose it wouldn't be a bad idea to learn that set theory.
So, can anyone offer advice, which one to learn?
It's Von Neumann–Bernays–Gödel set theory though, which I've heard is a lot nicer than ZFC, but I hear it rarely mentioned. People are always talking about ZFC, so I suppose it wouldn't be a bad idea to learn that set theory.
So, can anyone offer advice, which one to learn?
pboily
fingerlickinmathematickin
I really enjoyed Halmos' Naive Set Theory as an undergrad. http://en.wikipedia.org/wiki/Naive_Set_Theory_(book)
It's ZFC, which is still really nice when you get down to brass tracks. I'm not sure that there is any real advantage to learning Von Neumann-Bernays-Godel set theory instead of ZFC, although who's to say you wouldn't also find it interesting?
It's ZFC, which is still really nice when you get down to brass tracks. I'm not sure that there is any real advantage to learning Von Neumann-Bernays-Godel set theory instead of ZFC, although who's to say you wouldn't also find it interesting?
Thanks for the suggestion! I probably would have passed that book on a glance due to it's name.
Japanrocks12
tired of being a man
I'm having a little trouble understanding how to do arithmetic with complex numbers, the derivation to Euler's formula (the one with es and cosines), and what u(t) stands for in the situation that the Laplace transform of F(s) = 1/s is e^t times u(t).
ParadigmShifter
Random Nonsense Generator
Arithmetic is pretty easy, let z = a+ib, w = c+id
z+w = (a+c) + i(b+d)
z.w = (a+ib)(c+id) = ac + iad + ibc + i2bd = ac + i(ad + bc) + (-1)bd = (ac-bd) + i(ad+bc)
For division, define conjugate of z = a+ib as z* = a-ib
Then z.z* = a2 - iab + iab - i2b2
= a2 - (-1)b2 = a2 + b2
which is |z|2
so z.z* = |z|2 => z.z*/|z|2 = 1 => z-1 = z*/|z|2 (EDIT: Note, |z| is real so division is well defined)
To divide, w/z = w.z-1
Euler's formula comes from the power series expansion for sin and cos, multiply the series form of sin(x) by i and add it to the series for cos(x), you get the series for exp(ix)
I don't know about the Laplace transform, sorry.
z+w = (a+c) + i(b+d)
z.w = (a+ib)(c+id) = ac + iad + ibc + i2bd = ac + i(ad + bc) + (-1)bd = (ac-bd) + i(ad+bc)
For division, define conjugate of z = a+ib as z* = a-ib
Then z.z* = a2 - iab + iab - i2b2
= a2 - (-1)b2 = a2 + b2
which is |z|2
so z.z* = |z|2 => z.z*/|z|2 = 1 => z-1 = z*/|z|2 (EDIT: Note, |z| is real so division is well defined)
To divide, w/z = w.z-1
Euler's formula comes from the power series expansion for sin and cos, multiply the series form of sin(x) by i and add it to the series for cos(x), you get the series for exp(ix)
I don't know about the Laplace transform, sorry.
When doing complex arithmetic, you can just proceed like i was a variable, and at the end replace -1 for all i^2 (or powers bigger than that accordingly, so i^4 =(-1)^2=1 or i^6=(-1)^3 = -1).
If you want more intuitive understanding of it, the addition is like vector addition in R^2. The multiplication of two complex numbers a and b is a vector whose length is |a||b|, and angle from the real axis sum of angles of a and b.
Can you post the whole definition? Is u(t) perhaps the function that is transformed?
If you want more intuitive understanding of it, the addition is like vector addition in R^2. The multiplication of two complex numbers a and b is a vector whose length is |a||b|, and angle from the real axis sum of angles of a and b.
Can you post the whole definition? Is u(t) perhaps the function that is transformed?
IdiotsOpposite
Boom, headshot.
u(t) is the unit step function, of course. And on a related note...
How do you find the Laplace transform of a product of unit step functions?
How do you find the Laplace transform of a product of unit step functions?
Japanrocks12
tired of being a man
Thanks, Paradigm and Atticus, that was very helpful.
Yeah, u(t) is the step function, which I also think I understand now. Also, I made an error in my initial post, it should read "inverse Laplace transform"
Yeah, u(t) is the step function, which I also think I understand now. Also, I made an error in my initial post, it should read "inverse Laplace transform"
Complex addition and subtraction can easily be done on Cartesian coordinates (a+bi). For Complex multiplication and division, convert to polar notation(r<φ, and then it's easy. (r2<φ*(r2<φ2)=r1*r2<φ1+φ2. (r2<φ/(r2<φ2)=r1/r2<φ1-φ2. Where < is the angle sign.
, and then it's easy. (r2<φ*(r2<φ2)=r1*r2<φ1+φ2. (r2<φ/(r2<φ2)=r1/r2<φ1-φ2. Where < is the angle sign.
So it's 0 for t<0 and 1 for t>1? (I've encountered this by the name Heaviside function).
If it's indeed the aforementioned, why product? Aren't they all equal to the unit step function itself?
And just to make sure, this is the definition of Laplace transform we're talking about here:
Right?
IdiotsOpposite
Boom, headshot.
So it's 0 for t<0 and 1 for t>0? (I've encountered this by the name Heaviside function).
If it's indeed the aforementioned, why product? Aren't they all equal to the unit step function itself?
And just to make sure, this is the definition of Laplace transform we're talking about here:
Right?
FIFY, and yes, it is the Heaviside function.
Indeed it is, but the product I'm looking to transform is u(t)*u(10-t). And I'm not sure how to take a product like that.
ParadigmShifter
Random Nonsense Generator
Split it into separate cases.
Yeah, what ParadigmShifter said. Draw a picture of both functions, and figure out what their product might be. You don't usually do this kinds of products algebraically.
Define a non-horizontal, non-vertical line as its corresponding algebraic equation. Describe the addition of two such lines, the difference of two such lines, the product of two such lines, and supposing that no point of the line happens at x=0, what you get when you divide one such line by another such line.
duality of convolution and multiplication. Sorry about not being able to type up an equation easily, but you're looking for:
[/URL]
Step functions are quite easily obviously to see how that plays out.
But calling it the Heaviside function *cringes*
edit - really you're looking at the Laplace transform of a boxcar here so I googled that but didn't find a more convenient/easy trick to it, DTFT of course jogged my memory but I didn't feel like messing around more. Your product is obvious anyway before the transform and I'm sure it simplifies into something nice enough.
though you could go with the normalized boxcar/rectangular pulse and scale it and shift it then I guess, check your answer. (2/w sin(w/2)) I believe for the Fourier transform, guess I could work that out to s, I dunno, being lazy again here. Hope there was some help.
edit again - cancel any stupidity, just check wiki link which I somehow didn't find:
http://en.wikipedia.org/wiki/Rectangular_function
oh and actually splitting this into two step functions subtracted rather than multiplied is simpler yet, yeah, duh.
So [1-e^(-10s)]/ s ? Sorry to leave you hanging if that's not right
Mise
isle of lucy
It was named after a guy named Heaviside IIRC. Although the fact that it has a heavy side and an empty side is a nice easy way of remembering it...
p.s. the rect function causes much hilarity when lecturers use "E" (or even "A") as the function that's being multiplied by the rect function.
p.s. the rect function causes much hilarity when lecturers use "E" (or even "A") as the function that's being multiplied by the rect function.
Yes, I think he was Oliver Heaviside, British guy who was a forerunner of distribution theory, although not rigorous enough with them.
One another funny name is John. A set can be John, if it satisfies certain conditions that I don't now remember. The name comes from mathematician Fritz John. I heard that someone published a paper entitled "Julia is John", about the fractal set Julia, and another guy published "Julia is broad".
One another funny name is John. A set can be John, if it satisfies certain conditions that I don't now remember. The name comes from mathematician Fritz John. I heard that someone published a paper entitled "Julia is John", about the fractal set Julia, and another guy published "Julia is broad".
IdiotsOpposite
Boom, headshot.
Yes, Earthling, that's right. Thanks!
Now, there is one other question I dreamed up last night while I was asleep. The floor function is a discrete function. However, is the statement in the attachment true? Can the limit of a discrete function yield a continuous function?
Now, there is one other question I dreamed up last night while I was asleep. The floor function is a discrete function. However, is the statement in the attachment true? Can the limit of a discrete function yield a continuous function?
Similar threads
